【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
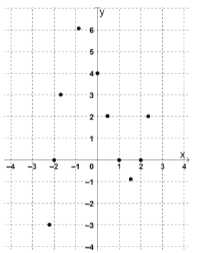
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.