题目内容
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.
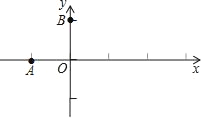
【答案】(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.
【解析】
(1)利用顶点式列出函数表达式,再将另一个点的坐标代入函数表达式列出一元一次方程,求出函数表达式.
(2)作出图象,结合图象思考.
解:(1)∵抛物线的顶点坐标为B(0,1)
∴设抛物线M的函数表达式为y=ax2+1
∵抛物线M经过点A(-1,0)
∴a×(-1)2+1=0,解得a=-1
∴抛物线M的函数表达为y=-x2+1
(2) ①由题意得,点F为BB1的中点
∵F(t,0),设B1的坐标为(m,n)
∴![]() ,
,![]()
∴m=2t,n=-1
∴B1(2t,-1).
②由题意可知抛物线M1的顶点B1的坐标为(2t,-1),二次项系数为1,
∴抛物线M1的函数表达式为:y=(x-2t)2-1(t>0),
当抛物线M1经过点A(-1,0)时(如下图):
∴(-1-2t)2-1=0,解得t1=-1,t2=0;

当抛物线M1经过点B(0,1)时(如上图):
∴(0-2t)2-1=1,解得t=![]() .
.
结合图象分析,因为t>0,所以当抛物线M1与线段AB有公共点时,t的取值范围是0<t≤![]() .
.
故答案为:(1) y=-x2+1;(2)①(2t,-1);②0<t≤![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目