��Ŀ����
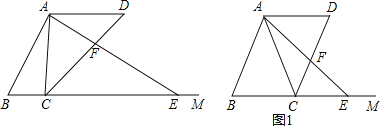
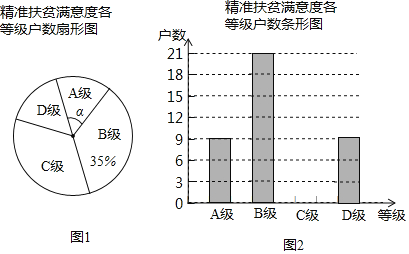
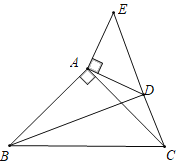
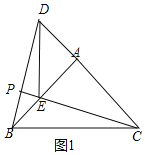
����Ŀ����ͼ����ABC�͡�ADE���й�������ĵ���ֱ�������Σ���BAC����DAE��90�㣬��PΪֱ��BD��CE�Ľ��㣮
��1����ͼ������ADE�Ƶ�A��ת����D���߶�CE��ʱ������BE�����и����������ۣ���BD��CD+![]() AD����BE2��2��AD2+AB2����������ȷ������ ����������֤����
AD����BE2��2��AD2+AB2����������ȷ������ ����������֤����
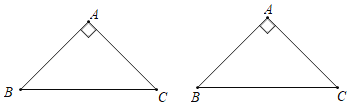
��2����AB��4��AD��2���ѡ�ADE�Ƶ�A��ת��
������EAC��90��ʱ����PB�ij���
����ת�������߶�PB�������ֵ���� ����
���𰸡���1������֤�������������2����PB��![]() ����2
����2![]() +2��
+2��
��������
��1����������֤����ABD�ա�ACE���Ϳ��Եõ����ۣ�����BDEΪֱ�������ξͿ��Եó�BE2��BD2+DE2������DAE����BAC�ǵ���ֱ�������ξ���DE2��2AD2��BC2��2AB2������BC2��BD2+CD2��BD2�Ϳ��Եó����ۣ�
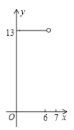
��2�����������ε���E��AB��ʱ��BE��AB��AE��2������PEB�ס�AEC����![]() ���ɴ˼��ɽ�����⣻����E��BA�ӳ�����ʱ��BE��6���ⷨ���ƣ�
���ɴ˼��ɽ�����⣻����E��BA�ӳ�����ʱ��BE��6���ⷨ���ƣ�
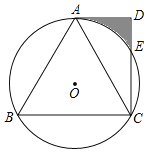
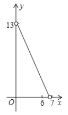
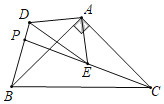
����ͼ3�У���AΪԲ��ADΪ�뾶��Բ����CE�ڡ�A�Ϸ����A����ʱ��PB��ֵ��ֱ����PB���ɣ�
��1���ߡ�ABC����ADE���й�������ĵ���ֱ�������Σ�
��AE��AD��AB��AC����DAE����BAC��90����DE��![]() AD��
AD��
���DAB����EAC����AE��AD��AB��AC��
���AEC�ա�ADB��SAS��
��BD��CE��DE+CD��
��BD��CD+![]() AD��
AD��
�����ȷ��
��BD��CE��
��BE2��BD2+DE2��
�ߡ�BAC����DAE��90����AB��AC��AD��AE��
��DE2��2AD2��BC2��2AB2��
��BC2��BD2+CD2��BD2��
��2AB2��BD2+CD2��BD2��
��BE2��2��AD2+AB2����
��ڴ���
�ʴ�Ϊ�٣�
��2����ͼ1�У�����E��AB��ʱ��BE��AB��AE��2��
�ߡ�EAC��90����
��CE��![]() ��
��![]() ��2
��2![]() ��
��
ͬ��1����֤��ADB�ա�AEC��
���DBA����ECA��
�ߡ�PEB����AEC��
���PEB�ס�AEC��
��![]() ��
��
��![]()
��PB��![]() ��
��
��ͼ2�У�����E��BA�ӳ�����ʱ��BE��AB+AE��6��

�ߡ�EAC��90����
��CE��![]() ��
��![]() ��2
��2![]() ��
��
ͬ��1����֤��ADB�ա�AEC��
���DBA����ECA��
�ߡ�BEP����CEA��
���PEB�ס�AEC��
��![]() ��
��
��![]() ��
��
��PB��![]() ��
��
���ϣ�PB��![]() ��
��![]() ��
��
����ͼ3�У���AΪԲ��ADΪ�뾶��Բ����CE�ڡ�A�Ϸ����A����ʱ��PB��ֵ���
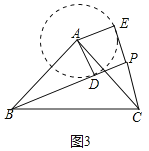
���ɣ���ʱ��BCE������PB�����PBC��ֱ�������Σ�б��BCΪ��ֵ����BCE������PB���
��AE��EC��
��EC��![]() ��
��![]() ��2
��2![]() ��
��
�ɣ�1����֪����ABD�ա�ACE��
���ADB����AEC��90����BD��CE��2![]() ��
��
���ADP����DAE����AEP��90����
���ı���AEPD�Ǿ��Σ�
��PD��AE��2��
��PB��BD+PD��2![]() +2��
+2��
����������PB�������ֵ��2![]() +2��
+2��
�ʴ�Ϊ��2![]() +2��
+2��