题目内容
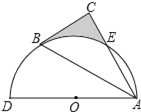
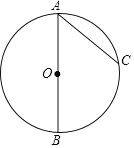
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)利用等腰三角形的性质证明∠BAE=2∠BAF,再证明∠EBD=∠BAF即可解决问题;
(2)作EH⊥BD于H.由sin∠BAF=sin∠EBD=![]() ,AB=5,推出BF=
,AB=5,推出BF=![]() ,推出BE=2BF=2
,推出BE=2BF=2![]() ,在Rt△BEH中,EH=BEsin∠EBH=2,推出BH=
,在Rt△BEH中,EH=BEsin∠EBH=2,推出BH=![]() =4,由EH∥AB,推出
=4,由EH∥AB,推出![]() ,由此即可求出DH解决问题;
,由此即可求出DH解决问题;
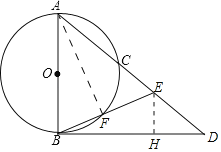
(1)证明:连接AF.
∵AB是直径,
∴∠AFB=90°,
∴AF⊥BE,
∵AB=AE,
∴∠BAE=2∠BAF,
∵BD是⊙O的切线,
∴∠ABD=90°,
∵∠BAF+∠ABE=90°,∠ABF+∠EBD=90°,
∴∠EBD=∠BAF,
∴∠BAE=2∠EBD.
(2)解:作EH⊥BD于H.
∵∠BAF=∠EBD,
∴sin∠BAF=sin∠EBD=![]() ,∵AB=5,
,∵AB=5,
∴BF=![]() ,
,
∴BE=2BF=2![]() ,
,
在Rt△BEH中,EH=BEsin∠EBH=2,
∴BH=![]() =4,
=4,
∵EH∥AB,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() ,
,
∴BD=BH+HD=![]() .
.

练习册系列答案
相关题目