Question

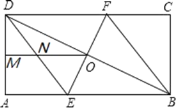
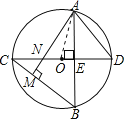
【题目】如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连接AD．

①AD_____AN（填“＞”，“＝”或“＜”）；

②AB＝8，ON＝1，⊙O的半径为_____．

Answer 1

【答案】=

【解析】

（1）根据圆周角定理得出∠BAD=∠BCD，在Rt△AEN和Rt△CMN得出∠BCD=∠BAM，再证明∠AND＝∠D，即可得出AN=AD；

（2）连接AO，先根据垂径定理求出AE的长，设OE=x，则NE=x+1，NE=ED=x+1，r=OD=OE+ED=2x+1，则AO=OD=2x+1，在Rt△AOE中根据勾股定理可得出x的值，进而得出结论．

（1）AD＝AN，

证明：∵CD⊥AB

∴∠CEB＝90°

∴∠C+∠B＝90°，

同理∠C+∠CNM＝90°

∴∠CNM＝∠B

∵∠CNM＝∠AND

∴∠AND＝∠B，

∵∠D＝∠B，

∴∠AND＝∠D，

∴AN＝AD，

（2）连接OA，设OE的长为x，

∵AN＝AD，CD⊥AB

∴DE＝NE＝x+1，

∴OD＝OE+ED＝x+x+1＝2x+1，

∴OA＝OD＝2x+1，

∴在Rt△OAE中OE2+AE2＝OA2，

∴x2+42＝（2x+1）2．

解得x＝或x＝﹣3（不合题意，舍去），

∴OA＝2x+1＝2×+1＝，

即⊙O的半径为，

故答案为：＝；．