题目内容
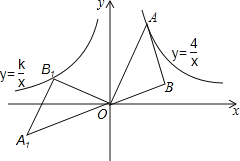
【题目】如图,A是反比例函数y=![]() (x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=
(x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=![]() 的图象经过点B1,则k的值是_____.
的图象经过点B1,则k的值是_____.
【答案】-2
【解析】
过点A作AE⊥y轴于点E,过点B1作BF⊥y轴于点F,则可证明△OB1F∽△OAE,设A(m,n),B1(a,b),根据三角形相似和等腰三角形的性质求得m=![]() .n=-
.n=-![]() a,再由反比例函数k的几何意义,可得出k的值.
a,再由反比例函数k的几何意义,可得出k的值.
过点A作AE⊥y轴于点E,过点B1作BF⊥y轴于点F,
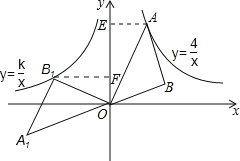
∵等腰直角△ABO绕点O以逆时针旋转135°,
∴∠AOB1=90°,
∴∠OB1F=∠AOE,
∵∠OFB1=∠AEF=90°,
∴△OB1F∽△OAE,
∴![]() =
=![]() =
=![]() ,
,
设A(m,n),B1(a,b),
∵在等腰直角三角形OAB中,![]() =
=![]() ,OB=OB1,
,OB=OB1,
∴![]() =
=![]() =
=![]() ,
,
∴m=![]() b.n=﹣
b.n=﹣![]() a,
a,
∵A是反比例函数y=![]() (x>0)图象上一点,
(x>0)图象上一点,
∴mn=4,
∴﹣![]() a
a![]() b=4,解得ab=﹣2.
b=4,解得ab=﹣2.
∵反比例函数y=![]() 的图象经过点B1,
的图象经过点B1,
∴k=﹣2.
故答案为:﹣2.

 优学名师名题系列答案
优学名师名题系列答案【题目】一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.