��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�?ABCO�Ķ���O��ԭ�㣬��A������Ϊ��-2��0������B������Ϊ��0��2������C�ڵ�һ���ޣ�
��1��ֱ��д����C�����ꣻ
��2����?ABCO�Ƶ�O��ʱ����ת��ʹOC����y����������ϣ���ͼ�ڣ��á�DEFG����D���O�غϣ���FG���AB��x��ֱ��ڵ�Q����P�����ʱ��תǰ������ƽ���ı����ص����ֵ����ΪS0����S0��ֵ��
��3��������2���еõ���?DEFG��x��������ƽ�ƣ����ƶ��Ĺ����У��趯��D������Ϊ��t��0����? DEFG��?ABCO�ص����ֵ����ΪS��д��S��t��0��t��2���ĺ�����ϵʽ����ֱ��д�������
DEFG��?ABCO�ص����ֵ����ΪS��д��S��t��0��t��2���ĺ�����ϵʽ����ֱ��д�������
��1��ֱ��д����C�����ꣻ
��2����?ABCO�Ƶ�O��ʱ����ת��ʹOC����y����������ϣ���ͼ�ڣ��á�DEFG����D���O�غϣ���FG���AB��x��ֱ��ڵ�Q����P�����ʱ��תǰ������ƽ���ı����ص����ֵ����ΪS0����S0��ֵ��
��3��������2���еõ���?DEFG��x��������ƽ�ƣ����ƶ��Ĺ����У��趯��D������Ϊ��t��0����?
 DEFG��?ABCO�ص����ֵ����ΪS��д��S��t��0��t��2���ĺ�����ϵʽ����ֱ��д�������
DEFG��?ABCO�ص����ֵ����ΪS��д��S��t��0��t��2���ĺ�����ϵʽ����ֱ��д���������1��C��2��2����
��2����A��-2��0����B��0��2��
��OA=OB=2
���BAO=��ABO=45��
��?EFGD��?ABCO��ת����
��DG=OA=2����G=��BAO=45��
��?EFGD
��FG��DE
���FPA=��EDA=90��
��Rt��POG�У�OP=OG•sin45��=
�ߡ�AQP=90��-��BAO=45��
��PQ=AP=OA-OP=2-
S0=
��PQ+OB��•OP=
��2-
+2��•
=2
-1��
��3��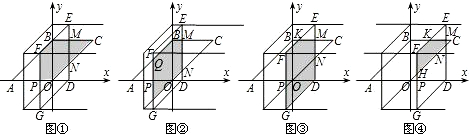
��?DEFG�˶�����F��AB��ʱ����ͼ�٣�t=2
-2
�ٵ�0��t��2
-2ʱ����ͼ�ڣ�S=-t2+
t+2
-1��
�ڵ�2
-2��t��
ʱ����ͼ�ۣ�S=-
t2+4
-3��
�۵�
��t��2ʱ����ͼ�ܣ�S=-
t+4
-2��
��2����A��-2��0����B��0��2��
��OA=OB=2
���BAO=��ABO=45��
��?EFGD��?ABCO��ת����
��DG=OA=2����G=��BAO=45��
��?EFGD
��FG��DE
���FPA=��EDA=90��
��Rt��POG�У�OP=OG•sin45��=
| 2 |
�ߡ�AQP=90��-��BAO=45��
��PQ=AP=OA-OP=2-
| 2 |
S0=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
��3��

��?DEFG�˶�����F��AB��ʱ����ͼ�٣�t=2
| 2 |
�ٵ�0��t��2
| 2 |
| 2 |
| 2 |
�ڵ�2
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
�۵�
| 2 |
| 2 |
| 2 |

��ϰ��ϵ�д�
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
�����Ŀ
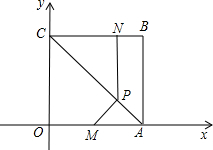

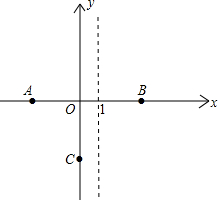


 Ϊԭ�㣬OA����ֱ��Ϊy�ᣬ��O�㴹ֱ��OA��ֱ��Ϊx�Ὠ��ֱ������ϵ����ˮ�絽б���ϵ���͵�ΪB����ߵ�ΪC��
Ϊԭ�㣬OA����ֱ��Ϊy�ᣬ��O�㴹ֱ��OA��ֱ��Ϊx�Ὠ��ֱ������ϵ����ˮ�絽б���ϵ���͵�ΪB����ߵ�ΪC��
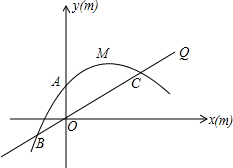
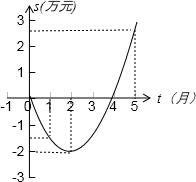 ���ۻ�����s����Ԫ��������ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�s��t֮��Ĺ�ϵ��������ͼ���ṩ����Ϣ������������⣺
���ۻ�����s����Ԫ��������ʱ��t���£�֮��Ĺ�ϵ����ǰt���µ������ܺ�s��t֮��Ĺ�ϵ��������ͼ���ṩ����Ϣ������������⣺