Question

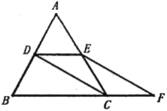
【题目】如图，四边形是正方形，点是边的中点，，且交正方形外角的平分线于点，试说明与的关系．

Answer 1

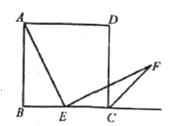
【答案】AE=EF，理由见解析

【解析】

取AB的中点G，连接EG，根据同角的余角相等得到∠BAE=∠CEF，证明△GAE≌△CEF即可；

AE=EF，
理由是：如图1，取AB的中点G，连接EG，则AG=BG，

∵四边形ABCD是正方形，BE=EC，
∴AG=BG=BE=EC，∠B=∠BCD=90°，
∴∠BAE+∠AEB=90°，∠BGE=45°，
∴∠AGE=135°，
∵CF是外角平分线，
∴∠DCF=45°，
∴∠ECF=135°，
∴∠AGE=∠ECF，
∵∠AEF=90°，
∴∠CEF+∠AEB=90°，
∴∠CEF=∠BAE，
在△AGE和△ECF中，
∵ ，
∴△AGE≌△ECF（ASA），
∴AE=EF