题目内容
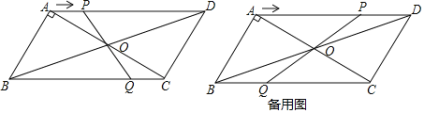
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=∠FDE=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图 (1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
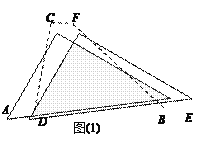
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图(3),△DEF的F点固定在AB的中点,然后绕F点按顺时针方向旋转△DEF,使EF交在AC边上于M,FD交BC于N,若FM=x,FN=y,试求y关于x的函数关系式。

【答案】(1) ![]() ,(2)略,(3)y=
,(2)略,(3)y=![]() x.
x.
【解析】试题分析:(1)过点C作![]() ,垂足是点
,垂足是点![]() ,易证四边形
,易证四边形![]() 是梯形,在直角
是梯形,在直角![]() 中利用三角形的性质求得
中利用三角形的性质求得![]() ,然后利用梯形的面积公式求解;
,然后利用梯形的面积公式求解;
(2)首先证明四边形![]() 是平行四边形,然后根据菱形的定义即可证得四边形
是平行四边形,然后根据菱形的定义即可证得四边形![]() 是菱形.
是菱形.
![]() 过点
过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() 由两组角分别对应相等,可得:
由两组角分别对应相等,可得: ![]() 对应边的比相等,可得出
对应边的比相等,可得出![]() 与
与![]() 的关系式.
的关系式.
试题解析:(1)过点C作CG⊥AE,垂足是点G.

由题可知,CF![]() AE,CF=AD=BE,
AE,CF=AD=BE,
则四边形CDBF是梯形.
∵在直角△ABC中, ![]()
∴AB=2,
在直角△ACG中, ![]()
![]()
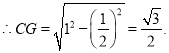
∴S梯形CDBF![]()
(2)四边形CDBF是菱形.
理由如下:∵在直角△ABC中,D是AB的中点,
∴AD=DB=CD,
由(1)CF=AD,
∴CF=DB=CD,
又∵CF![]() AE,
AE,
∴四边形CDBF是平行四边形.
∵CD=BD,
∴四边形CDBF是菱形.
![]() 过点
过点![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]()
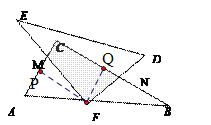
![]()
可解得![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
即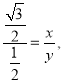 整理得:
整理得: ![]()

【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
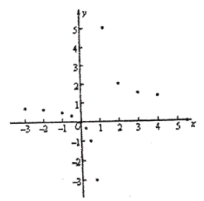
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .