题目内容
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
【答案】(1)20;(2)当每件衬衫降价16元时,专卖店每天获得的利润最大,最大利润是1440元
【解析】试题分析:(1)设每件衬衫降价x元,根据题意列出方程,解方程即可得到x的值;
(2)用“配方法”即可求出y的最大值,即可得到每件衬衫降价多少元.
试题解析:(1)设每件衬衫降价x元,
则(40﹣x)(20+![]() x)=1400,
x)=1400,
解得 x1=12,x2=20,
经检验,x1=10,x2=20都是原方程的解,但要尽快减少库存,
所以x=20,
答:每件衬衫应降价20元;
(2)设每件衬衫降价x元,商场平均每天盈利y元,
∵y=(40﹣x)(20+![]() x)=﹣
x)=﹣![]() (x﹣16)2+1440,
(x﹣16)2+1440,
∴当x=16时,y的最大值为1440,
答:当每件衬衫降价16元时,专卖店每天获得的利润最大,最大利润是1440元.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
【题目】为了传承优秀传统文化,我市组织了一次七年级1200名学生参加的“汉字听写”大赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:
组别 | 成绩分组 | 频数 | 频率 |
A | 35≤x<38 | 3 | 0.03 |
B | 38≤x<41 | a | 0.12 |
C | 41≤x<44 | 20 | 0.20 |
D | 44≤x<47 | 35 | 0.35 |
E | 47≤x≤50 | 30 | b |
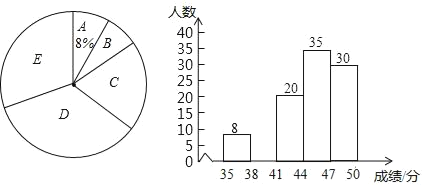
请根据所提供的信息解答下列问题:
(1)频率统计表中a= ,b= ;
(2)请补全频数分布直方图;
(3)在扇形统计图中D组的圆心角是 度;
(4)请根据抽样统计结果,估计该次大赛中成绩不低于41分的学生有多少人?