��Ŀ����
����Ŀ��ijУ�����ƽ����������������̣���ѧ���ھ��꼶11�����п�չ����ѭ��������ÿ������������ֱ����һ��������ÿ�������10������������������涨��ÿ��������Ҫ�ֳ�ʤ����ʤһ����3�֣���һ���é�1�֣�
��1�����ij�������еı�����ֻ��14�֣���ô�ð�ʤ�������ֱ��Ƕ��٣�
��2��������������װ�÷����Ұ��3�����װ��ʤ�ij���������5�����Ҽװ��ʤ�ij��������Ұ࣬��������װࡢ�Ұ��ʤ�˼�����
���𰸡���1���ð�ʤ6������4������2���װ�ʤ4�����Ұ�ʤ3����
��������
��1����ð�ʤx������ðฺ��10��x�������������3x����10��x����14��2����װ�ʤ��x�����Ұ�ʤ��y�����������У�3x����10��x����3[3y����10��y��]�����������ݲ���ʽ���ʣ�����Ǹ�����x,y.
�⣺��1����ð�ʤx������ðฺ��10��x������
�������3x����10��x����14
��֮��x��6
���Ըð�ʤ6������4����
��2����װ�ʤ��x�����Ұ�ʤ��y�����������У�
3x����10��x����3[3y����10��y��]��
����3y��x+5��
��y��![]() ��
��
����x��y�ǷǸ���������0��x��5��x��y��
��x��4��y��3��
���Լװ�ʤ4�����Ұ�ʤ3����
�𣺣�1���ð�ʤ6������4������2���װ�ʤ4�����Ұ�ʤ3����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���![]() ��ͼ������ʽ�����̽����̽���������£��벹��������
��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���![]() ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��
��2���±���![]() ��
��![]() �ļ����Ӧ��ֵ��
�ļ����Ӧ��ֵ��
| �� |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | �� |
| �� |
|
|
|
| 0 |
|
|
|
| 2 |
|
| �� |
��д��![]() ��ֵΪ ��
��ֵΪ ��
����ƽ��ֱ������ϵ�У�������Ա��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
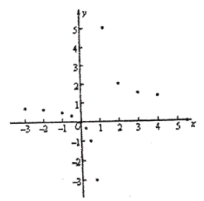
��3����![]() ʱ��ֱ��д��x��ȡֵ��ΧΪ�� ��
ʱ��ֱ��д��x��ȡֵ��ΧΪ�� ��