题目内容
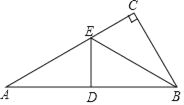
【题目】如图,在Rt△ABC中,∠C=90°,D是AB的中点,E在边AC上,若D与C关于BE成轴对称,则下列结论:①∠A=30°;②△ABE是等腰三角形;③点B到∠CED的两边距离相等.其中正确的有( )
A. 0个B. 1个C. 2个D. 3个
【答案】D
【解析】
根据题意需要证明Rt△BCE≌Rt△BDE, Rt△EDA≌Rt△EDB,即可解答
∵D与C关于BE成轴对称
∴Rt△BCE≌Rt△BDE(SSS)
∵△BCE≌△BDE
∴∠EDB=∠EDA=90°,BD=BC
又∵D是AB的中点
∴AD=DB
∴Rt△EDA≌Rt△EDB(HL)
∴∠A=30°(直角三角形含30°角,BC=![]() AB)
AB)
∴△ABE是等腰三角形
∴点B到∠CED的两边距离相等
故选D

练习册系列答案
相关题目
【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.