题目内容
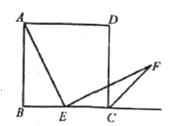
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的顶点A在△ECD的斜边DE上,连接BD.

(1)求证:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据同角的余角相等得出∠BCD=∠ACE,然后根据SAS定理证明△BCD≌△ACE,从而得出结论;
(2)根据全等三角形的性质得出∠BDC=∠AEC,然后结合等腰直角三角形的性质求得∠BDA是直角三角形,从而利用勾股定理求解.
(1)∵△ACB和△ECD都是等腰直角三角形
∴∠ACB=∠ECD=90°
∴∠ACD+∠BCD=90°,∠ACD+∠ACE=90°
∴∠BCD=∠ACE
在△BCD和△ACE中
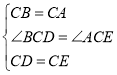
∴△BCD≌△ACE(SAS)
∴BD=AE
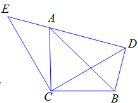
(2)∵△BCD≌△ACE
∴∠BDC=∠AEC
又∵△ECD是等腰直角三角形
∴∠CDE=∠CED=45°
∴∠BDC=45°
∴∠BDC+∠CDE=90°
∴∠BDA是直角三角形
∴![]()
在等腰直角三角形ACB中
![]()
∴![]()

练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
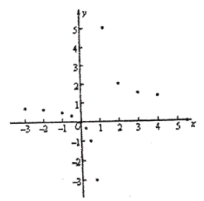
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .