题目内容
【题目】如图，在等边
中，
分别为
的中点，延长
至点
，使
，连结
和
．
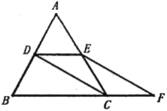
（1）求证：
（2）猜想：的面积与四边形
的面积的关系，并说明理由．
【答案】（1）见解析；（2）相等，理由见解析．
【解析】
（1）直接利用三角形中位线定理得出DE∥BC，且DE=
BC，再利用平行四边形的判定方法得出答案；
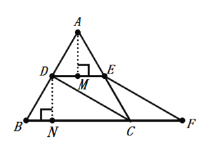
（2）分别过点A，D，作AM⊥DE，DN⊥BC，根据等底等高的三角形面积相等求得S△ADE=S△ECF，再根据S△ADE +S四边形BDEC=S△ECF +S四边形BDEC可得出结果．
（1）证明：∵D，E分别为AB，AC的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE＝BC．
∵CF＝BC，
∴DE∥CF，DE=CF，
∴四边形DEFC为平行四边形，
∴CD=EF；
（2）解：相等．理由如下：
分别过点A，D，作AM⊥DE，DN⊥BC，则∠AMD=∠DNB=90°，
∵DE∥BC，
∴∠ADM=∠DBN．
∵AD=DB，
∴△ADM≌△DBN(AAS)，
∴AM=DN．
又∵DE=CF，
∴S△ADE=S△ECF （等底等高的三角形面积相等）．
∴S△ADE +S四边形BDEC=S△ECF +S四边形BDEC，
∴△ABC的面积等于四边形BDEF的面积．
练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数
的图象和性质进行了探究，探究过程如下，请补充完整：
（1）自变量
的取值范围是__________；
（2）下表是
与的几组对应数值：
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出
的值为 ；
②在平面直角坐标系中，描出了以表中各对对应值为坐标的点，根据描出的点，画出该函数的图象：
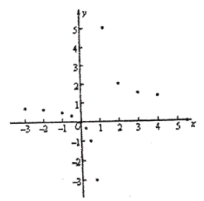
（3）当
时，直接写出x的取值范围为： ．
