Question

【题目】如图，在菱形ABCD中，AB=BD，点E，F分别在AB，AD上，且AE=DF,连接BF与DE相交于点G，连接CG与BD相交于点H,下列结论：

①△AED≌△DFB；②S四边形 BCDG=CG2；③若AF=2DF，则BG=6GF

,其中正确的结论

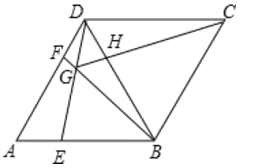
A.只有①②.B.只有①③.C.只有②③.D.①②③.

Answer 1

【答案】D

【解析】

解：①∵ABCD为菱形，∴AB=AD．

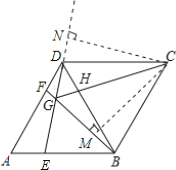
∵AB=BD，∴△ABD为等边三角形．

∴∠A=∠BDF=60°．

又∵AE=DF，AD=BD，

∴△AED≌△DFB；

②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD，

即∠BGD+∠BCD=180°，

∴点B、C、D、G四点共圆，

∴∠BGC=∠BDC=60°，∠DGC=∠DBC=60°．

∴∠BGC=∠DGC=60°．

过点C作CM⊥GB于M，CN⊥GD于N．

∴CM=CN，

则△CBM≌△CDN，（HL）

∴S四边形BCDG=S四边形CMGN．

S四边形CMGN=2S△CMG，

∵∠CGM=60°，

∴GM=CG，CM=CG，

∴S四边形CMGN=2S△CMG=2××CG×CG=CG2．

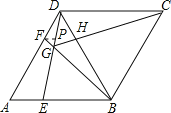
③过点F作FP∥AE于P点．

∵AF=2FD，

∴FP：AE=DF：DA=1：3，

∵AE=DF，AB=AD，

∴BE=2AE，

∴FP：BE=1：6=FG：BG，

即 BG=6GF．

故选D．