Question

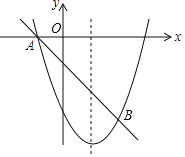
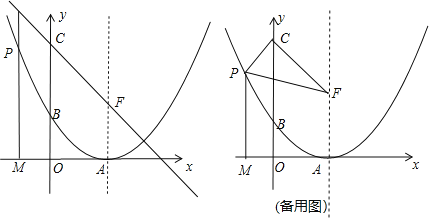
【题目】如图，抛物线与轴交于两点，与轴交于点．

（1）求抛物线的解析式；

（2）点是抛物线上的动点，且满足，求出点的坐标；

（3）连接，点是轴一动点，点是抛物线上一动点，若以、、、为顶点的四边形是平行四边形时，请直接写出点的坐标．

备用图

Answer 1

【答案】（1）;（2），，，；（3），，

【解析】

（1）由待定系数法求出解析式即可；

（2）先求出点C坐标，可得OA=OC=3，由面积关系列出方程即可求解；

（3）分两种情况讨论，利用平行四边形的性质可求解；

解：

（1）∵抛物线经过点A（-3，0），点B（1，0），

∴，

解得：，

∴抛物线的解析式为：，

∵抛物线的解析式为：，与y轴交于点C，

∴点C坐标为（0，3），

即OA=OC=3；

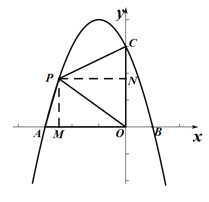
（2）过点P作PM⊥AO于点M，PN⊥CO于点N，

设P(，)，

∵ ，

∴，

∵AO=3，CO=3，

∴PM=2PN，即，

当点P在第一、三象限时，，

解得，，；

∴，，

当点P在第二、四象限时，，

解得，；

∴，；

（3）若BC为边，且四边形BCFE是平行四边形，

∴CF∥BE，

∴点C与点F纵坐标相等，

∴，

解得，（舍去），

∴点F（-2，3），

若BC为边，且四边形BCFE是平行四边形，

∴BE与CF互相平分，

∵BE中点纵坐标为0，且点C纵坐标为3，

∴点F的纵坐标为-3，

∴，

解得，

∴，，

∴或，

若BC为对角线,则四边形BECF是平行四边形，

∴BC与EF互相平分，

∴BC中点纵坐标为，且点E的纵坐标为0，

∴点F的纵坐标为3，

∴点F（-2，3），

综上所述，点F坐标为：，，；