Question

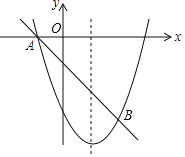
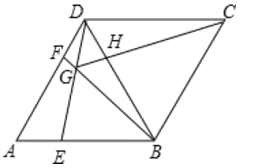
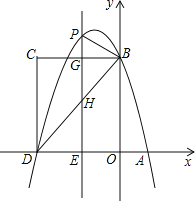
【题目】正方形ABCD与正方形DEFG按如图1放置，点A，D，G在同一条直线上，点E在CD边上，AD＝3，DE＝，连接AE，CG

（1）线段AE与CC的关系为______；

（2）将正方形DEFG绕点D顺时针旋转一个锐角后，如图2，请问（1）中的结论是否仍然成立？请说明理由

（3）在正方形DEFG绕点D顺时针旋转一周的过程中，当∠AEC＝90°时，请直接写出AE的长．

Answer 1

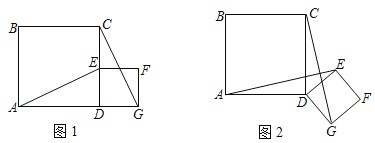
【答案】（1）AE＝CG，AE⊥CG；（2）仍然成立；理由见解析；（3）AE的长为2+1或2﹣1．

【解析】

（1）延长AE交CG于点H，证△ADE≌△CDG，可得到AE＝CG，∠EAD＝∠GCD，再证∠CHE＝90°，即可得出结论；

（2）设AE与CG交于点H，证∴△ADE≌△CDG，可得到AE＝CG，∠EAD＝∠GCD，再证，∠CHP＝90°，即可得出结论；

（3）分两种情况讨论，当点E旋转到线段CG上时，过点D作DM⊥AE于点M，构造等腰直角三角形DME和直角三角形ADM，可通过勾股定理分别求出ME，AM的长即可；当点E旋转到线段CG的延长线上时，过点D作DN⊥CE于点N，构造等腰直角三角形DNE和直角三角形CND，可通过勾股定理分别求出NE，CN的长，再求出CE的长，在Rt△AEC中通过勾股定理可求出AE的长．

（1）线段AE与CG的关系为：AE＝CG，AE⊥CG，

理由如下：

如图1，延长AE交CG于点H，

∵四边形ABCD和四边形DGFE是正方形，

∴AD＝CD，ED＝GD，∠ADE＝∠CDG＝90°，

∴△ADE≌△CDG（SAS），

∴AE＝CG，∠EAD＝∠GCD，

∵∠EAD+∠AED＝90°，∠AED＝∠CEH，

∴∠GCD+∠CEH＝90°，

∴∠CHE＝90°，即AE⊥CG，

故答案为：AE＝CG，AE⊥CG；

（2）结论仍然成立，理由如下：

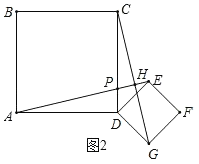
如图2，设AE与CG交于点H，

∵四边形ABCD和四边形DGFE是正方形，

∴AD＝CD，ED＝GD，∠ADC＝∠EDG＝90°，

∴∠ADC+∠CDE＝∠EDG+∠CDE，

即∠ADE＝∠CDG，

∴△ADE≌△CDG（SAS），

∴AE＝CG，∠EAD＝∠GCD，

∵∠EAD+∠APD＝90°，∠APD＝∠CPH，

∴∠GCD+∠CPH＝90°，

∴∠CHP＝90°，即AE⊥CG，

∴AE＝CG，AE⊥CG，

∴①中的结论仍然成立；

（3）如图3﹣1，当点E旋转到线段CG上时，过点D作DM⊥AE于点M，

∵∠AEC＝90°，∠DEG＝45°，

∴∠AED＝45°，

∴Rt△DME是等腰直角三角形，

∴ME＝MD＝DE＝1，

在Rt△AMD中，ME＝1，AD＝3，

∴AM＝＝＝2，

∴AE＝AM+ME＝2+1；

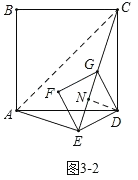
如图3﹣2，当点E旋转到线段CG的延长线上时，过点D作DN⊥CE于点N，

则∠END＝90°，

∵∠DEN＝45°，

∴∠EDN＝45°，

∴Rt△DNE是等腰直角三角形，

∴NE＝ND＝DE＝1，

在Rt△CND中，ND＝1，CD＝3，

∴CN＝＝＝2，

∴CE＝NE+CN＝2+1，

∵AC＝AD＝3，

∴在Rt△AEC中，

AE＝＝＝2﹣1，

综上所述，AE的长为2+1或2﹣1．