题目内容
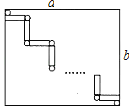
【题目】如图由长为a,宽为b的矩形、(2m+1)个长为4,宽为1的小矩形(为正整数)和若干个小圆组成,其中小圆的直径与小矩形的宽相等.
(1)当m=1时,a= ,b= ;
(2)当a=24时,求b的值;
(3)a的值能否等于30?请通过计算说明理由;
(4)直接写出a与b的数量关系.
【答案】(1)9,7;(2)22;(3)![]() 不能等于30,见解析;(4)
不能等于30,见解析;(4)![]()
【解析】
(1)长为![]() ,宽为
,宽为![]() 的矩形,当
的矩形,当![]() =1时,(2
=1时,(2![]() +1)=3,得3个长为4,宽为1的小矩形(为正整数)和5个小圆组成,其中小圆的直径与小矩形的宽相等,进而求解;
+1)=3,得3个长为4,宽为1的小矩形(为正整数)和5个小圆组成,其中小圆的直径与小矩形的宽相等,进而求解;
(2)结合(1)并观察图形的变化规律可得![]() =5
=5![]() +4,b=5
+4,b=5![]() +2,进而求解;
+2,进而求解;
(3)![]() 不能等于30,根据
不能等于30,根据![]() =5
=5![]() +4当
+4当![]() =30,可求5
=30,可求5![]() +4=30,进而得
+4=30,进而得![]() 的值即可判断;
的值即可判断;
(4)结合(1)(2)可得![]() .
.
(1)长为![]() ,宽为
,宽为![]() 的矩形,
的矩形,
当![]() =1时,(2
=1时,(2![]() +1)=3,
+1)=3,
3个长为4,宽为1的小矩形(为正整数)和5个小圆组成,
其中小圆的直径与小矩形的宽相等,
∴![]() =3+3+1+1+1=9
=3+3+1+1+1=9
![]() =3+1+1+1+1=7
=3+1+1+1+1=7
故答案为9,7;
(2)结合(1)并观察图形的变化规律可知:
![]() =5
=5![]() +4,b=5
+4,b=5![]() +2
+2
∴当![]() =24时,5
=24时,5![]() =20,
=20,
∴![]() =22;
=22;
(3)![]() 不能等于30,理由如下:
不能等于30,理由如下:
∵![]() =5
=5![]() +4
+4
若![]() =30,则5
=30,则5![]() +4=30,
+4=30,![]() =
=![]()
∵![]() 是正整数,
是正整数,
∴![]() 不能等于30;
不能等于30;
(4)结合(1)(2)可知:
![]() ,
,
所以![]() 与
与![]() 的数量关系为:
的数量关系为:![]() .
.

【题目】如表是我国运动员在最近六届奥运会上所获奖牌总数情况:
届数 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |
31 | 26 | 18 | 26 | 70 |
数学小组分析了上面的数据,得出这六届奥运会我国奖牌总数的平均数、中位数如表所示:
统计量 | 平均数 | 中位数 |
数值 | 约为71.67 | m |
(1)上表中的中位数m的值为 ;
(2)经过数学小组的讨论,认为由于第29届奥运会在我国北京召开,我国运动员的成绩超常,所以其数据应记为极端数据,在计算平均数时应该去掉,于是计算了另外五属奥运会上我国奖总数的平均数,这个平均数应该是
(3)根据上面提供的信息,预估我国运动员在2020年举行的第32届奥运会上将获得多少枚奖牌,并写出你的预估理由