题目内容
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)根据矩形的性质得到AE∥OC,AE=OC即可证明;
(2)根据平行四边形的性质得到∠AOD=∠OCF,∠AOF=∠OFC,再根据等腰三角形的性质得到∠OCF=∠OFC.故可得∠AOD=∠AOF,利用SAS证明△AOD≌△AOF,由ADO=90°得到AH⊥OF,即可证明;
(3)根据切线长定理可得AD=AF,CH=FH=2,设AD=x,则AF=x,AH=x+2,BH=x-2,再利用在Rt△ABH中,AH2=AB2+BH2,代入即可求x,即可得到AH的长.
(1)解:连接AO,四边形AECO是平行四边形.
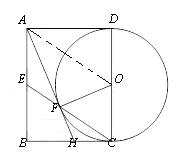
∵四边形ABCD是矩形,
∴AB∥CD,AB=CD.
∵E是AB的中点,
∴AE=![]() AB.
AB.
∵CD是⊙O的直径,
∴OC=![]() CD.∴AE∥OC,AE=OC.
CD.∴AE∥OC,AE=OC.
∴四边形AECO为平行四边形.
(2)证明:由(1)得,四边形AECO为平行四边形,
∴AO∥EC
∴∠AOD=∠OCF,∠AOF=∠OFC.
∵OF=OC
∴∠OCF=∠OFC.
∴∠AOD=∠AOF.
∵在△AOD和△AOF中,AO=AO,∠AOD=∠AOF,OD=OF
∴△AOD≌△AOF.
∴∠ADO=∠AFO.
∵四边形ABCD是矩形,
∴∠ADO=90°.
∴∠AFO=90°,即AH⊥OF.
∵点F在⊙O上,
∴AH是⊙O的切线.
(3)∵HC、FH为圆O的切线,AD、AF是圆O的切线
∴AD=AF,CH=FH=2,
设AD=x,则AF=x,AH=x+2,BH=x-2,
在Rt△ABH中,AH2=AB2+BH2,
即(x+2)2=62+(x-2)2,
解得x=![]()
∴AH=![]() +2=
+2=![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案