Question

【题目】已知关于x的方程|x2+2px﹣3p2+5|﹣q＝0，其中p、q都是实数．

（1）若q＝0时，方程有两个不同的实数根x1x2，且，求实数p的值．

（2）若方程有三个不同的实数根x1、x2、x3，且，求实数p和q的值．

Answer 1

【答案】（1）p＝5；（2），q＝3．

【解析】

（1）根据根与系数的关系可得△＝（2p）2﹣4（﹣3p2+5）＝16p2﹣20＞0，x1+x2＝﹣2p，，代入可得关于p的方程，解方程即可；

（2）由方程有三个不同的实数根x1、x2、x3，可得x3＝﹣p，x1、x2是方程x2+2px﹣3p2+5＝q的两根；由根与系数的关系可得x1+x2＝﹣2p，，x3＝﹣p．△＝（2p）2﹣4（﹣7p2+10）＝32p2﹣40＞0，进而得到关于p的方程，解出p即可求出q的值．

解：（1）若q＝0，则方程为x2+2px﹣3p2+5＝0．

因该方程有两个不同的实数x1、x2，

可得△＝（2p）2﹣4（﹣3p2+5）＝16p2﹣20＞0，x1+x2＝﹣2p，

解得p2＞；

由，得，

解得p＝5或．（注意5﹣3p2≠0）

因为p2＞，所以p＝5．

（2）显然q＞0．方程可写成x2+2px﹣3p2+5＝±q．

因该方程有三个不同的实数根，

即函数与y2＝±q的图象有三个不同的交点，

∴可得：，

即q＝4p2﹣5．x1、x2是方程x2+2px﹣3p2+5＝q的两根，

即x2+2px﹣7p2+10＝0．

则x1+x2＝﹣2p，，x3＝﹣p．

△＝（2p）2﹣4（﹣7p2+10）＝32p2﹣40＞0，

解得p2＞．

由，得，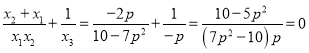

解得p2＝2＞，

所以，q＝4p2﹣5＝3．