题目内容
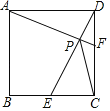
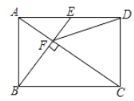
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF.其中正确的结论有( )个
S△ABF.其中正确的结论有( )个
A.4B.3C.2D.1
【答案】A
【解析】
①四边形ABCD是矩形,BE⊥AC,则∠ABC=∠AFB=90°,又∠BAF=∠CAB,于是△AEF∽△CAB,故①正确;
②由![]() ,又AD∥BC,所以
,又AD∥BC,所以![]() ,进而得出
,进而得出![]() ,故②正确;
,故②正确;
③过D作DM∥BE交AC于N,得到四边形BMDE是平行四边形,求出BM=DE=1212BC,得到CN=NF,根据线段的垂直平分线的性质可得结论,故③正确;
④根据相似三角形的边长之比得出△ABF和△ABC的比值,从而得出四边形CDEF和△ABF的面积之比,即可判定④正确.
过D作DM∥BE交AC于N,如图所示:

∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正确;
∵AD∥BC,
∴△AEF∽△CBF,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() ,
,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于点F,DM∥BE,
∴DN⊥CF,
∴DF=DC,故③正确;
∵![]()
∴![]() ,
,![]()
∵![]()
设![]() ,则
,则![]() ,S四边形CDEF=
,S四边形CDEF=![]()
∴S四边形CDEF=![]() S△ABF,故④正确;
S△ABF,故④正确;
故选:A.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案【题目】洛阳某科技公司生产和销售A、B两类套装电子产品![]() 已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元
已知3套A类产品和2套B类产品的总售价是24万元;2套A类产品和3套B类产品的总售价是26万元![]() 公司生产一套A类产品的成品是
公司生产一套A类产品的成品是![]() 万元,生产B类产品的成本如下表:
万元,生产B类产品的成本如下表:
套数 | 1 | 2 | 3 | 4 |
|
总成本 | 8 | 12 | 16 | 20 |
|
![]() 该公司A类产品和B类产品的销售单价分别是多少万元?
该公司A类产品和B类产品的销售单价分别是多少万元?
![]() ①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润
①公司为了方便生产,只安排生产一类电子产品,且销售顺利,设生产销售该类电子产品x套:公司销售x套A类产品的利润![]() ________;公司销售x套B类产品的利润
________;公司销售x套B类产品的利润![]() ________.
________.
②怎样安排生产,才能使公司获得的利润较高?