Question

【题目】若n是一个两位正整数，且n的个位数字大于十位数字，则称n为“两位递增数”（如13，35，56等）．在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6构成的所有的“两位递增数”中随机抽取1个数，且只能抽取一次．

（1）写出所有个位数字是5的“两位递增数”；

（2）请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率．

Answer 1

【答案】（1）15、25、35、45；（2）.

【解析】试题分析：（1）根据“两位递增数”定义可得；（2）画树状图列出所有“两位递增数”，找到个位数字与十位数字之积能被10整除的结果数，根据概率公式求解可得．

试题解析：

（1）根据题意所有个位数字是5的“两位递增数”是15、25、35、45这4个；

（2）画树状图为：

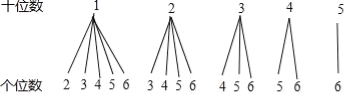
共有15种等可能的结果数，其中个位数字与十位数字之积能被10整除的结果数为3，

所以个位数字与十位数字之积能被10整除的概率=．