题目内容
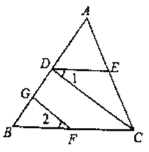
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,延长
的中点,延长![]() 到点
到点![]() ,使
,使![]() ,得四边形
,得四边形![]() .若使四边形
.若使四边形![]() 是正方形,则应在
是正方形,则应在![]() 中再添加一个条件为__________.
中再添加一个条件为__________.

【答案】答案不唯一,如∠ACB=90° 或∠BAC=45°或∠B=45°
【解析】
先证明四边形ADCF是平行四边形,再证明AC=DF即可,再利用∠ACB=90°得出答案即可.
∠ACB=90°时,四边形ADCF是正方形,
理由:∵E是AC中点,
∴AE=EC,
∵DE=EF,
∴四边形ADCF是平行四边形,
∵AD=DB,AE=EC,
∴DE=![]() BC,
BC,
∴DF=BC,
∵CA=CB,
∴AC=DF,
∴四边形ADCF是矩形,
点D. E分别是边AB、AC的中点,
∴DE//BC,
∵∠ACB=90°,
∴∠AED=90°,
∴矩形ADCF是正方形.
故答案为∠ACB=90°.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目