题目内容
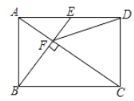
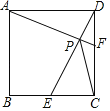
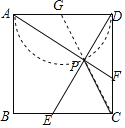
【题目】如图,正方形ABCD的边长为4,点E、F分别是BC,CD边上的动点,且CE+CF=4,DE和AF相交于点P,在点E,F运动的过程中,CP的最小值为_____.
【答案】2![]() ﹣2
﹣2
【解析】
根据正方形的性质得到AD=CD=BC=4,∠ADC=∠BCD=90°,求得CE=DF,根据全等三角形的性质得到∠DAF=∠CDE,推出∠APD=90°,得到点P在以AD为直径的圆上,设AD的中点为G,由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:根据勾股定理即可得到结论.
解:在正方形ABCD中,AD=CD=BC=4,∠ADC=∠BCD=90°,
∵CE+CF=4,CF+DF=4,
∴CE=DF,
在△ADF和△DCE中,
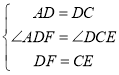 ,
,
∴△ADF≌△DCE(SAS),
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=90°,
∴∠DAP+∠FDP=90°,
∴∠APD=90°,
∴点P在以AD为直径的圆上,
设AD的中点为G,
由图形可知:当C、P、G在同一直线上时,CP有最小值,如图所示:
∵CD=4,DG=2,
∴CG=![]() =2
=2![]()
∴CP=CG﹣PG=2![]() ﹣2,
﹣2,
故答案为:2![]() ﹣2.
﹣2.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目