Question

【题目】阅读下面材料，并回答问题：

定义：平面内与一个定点F和一条定直线l（l不经过点F）距离相等的所有点组成的图形叫抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．

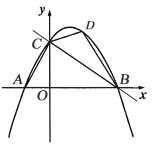
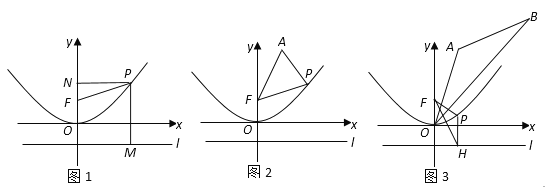
应用：（1）如图1，一条抛物线的焦点为F(0，1)，准线为过点(0，-1)且平行于x轴的直线l；设点P(x，y)为抛物线上任意一点，小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答，请你将余下部分补充出来．

解：设点P(x，y)为抛物线上任意一点，作PM⊥l于点M，则PM=_________

作PN⊥y轴于点N，则在△PFN中，有PN=，NF=，所以PF=__________

∵PF=PM

∴_________=____________，

将方程两边同时平方，解得抛物线的解析式为_____________

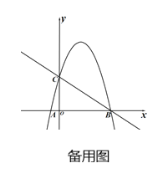
（2）如图2，在（1）的条件下，点A(1，3)是坐标平面内一点，则△FAP的周长最小值为________

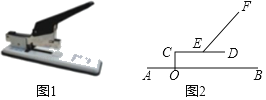
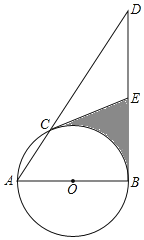
（3）在（1）（2）的条件下，如图3，点B(4，4)是坐标平面内另一点，过P作PH⊥l，垂足为H，连接PF和FH，问在抛物线上是否存在点P，使得以P，F，H为顶点的三角形与△ABO相似？若存在，求出P点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y+1，，y+1，，；（2）；（3）存在，(1，)或(﹣1，)

【解析】

(1)设点P(x，y)为抛物线上任意一点，作PM⊥l于点M，根据抛物线的定义PF=PM以及两点间的距离公式得到=，即可求解；

(2)抛物线的定义知PF=PM，为定长，故当点A、P、M在同一直线上时，△FAP的周长最小，利用两点间的距离公式即可求得最小值；

(3)根据两点间的距离公式求得AB= AO=，由抛物线的定义知PF=PH，再根据相似三角形的性质得到，即可求解．

(1)设点P(，)为抛物线上任意一点，作PM⊥于点M，则PM=，

作PN⊥y轴于点N，则在△PFN中，有PN=，NF=，所以PF=，

∵PF=PM，

∴=，

将方程两边同时平方，解得抛物线的解析式为；

故答案为：y+1，，y+1，，；

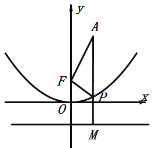
(2)∵PF=PM，

∴点A、P、M在同一直线上时，△FAP的周长最小，如图：

，，

∴△FAP的周长最小值为：；

(3)存在，理由如下：

∵AB==，AO==，OB==4，

∴AB=OA，

∵PF=PH，

假设存在这样的点P，使得以P，F，H为顶点的三角形与△ABO相似，

则PH与AB，FH与OB是对应边，

∴，

设点P(m，m2)，则H为(m，-1)，

则，

∴，

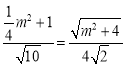解得：，

∴点P坐标(1，)或(﹣1，)．