��Ŀ����
����Ŀ������������ƶ������а塢ѹ��������������λ�����ɣ���ͼ1��һ̨������ˮƽ�����ϵĴ��Ͷ�������������������ͼ2��ʾ�ļ���ͼ�Σ���ѹ����EF�Ķ˵�E�̶��ڶ�λ��CD���е㴦����ʹ�ù����У���D�͵�F��ѹ��������λ���Ƶ�C��ת��CO��AB�ڵ�O��CD��12cm����CF������FED��45������FCD��30����
��1����FC�ij���
��2����OC��2cm����ʹ�ù����У�����D���ڵ���AB��ʱ�������CD��AB�ļнǼ���F�˶���·��֮�����������ȷ��0.1cm���ο����ݣ�sin9.6���0.17���С�3.14��![]() 1.732��
1.732��
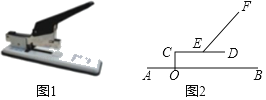
���𰸡���1��CF��16.4cm����2��CD��AB�ļн�Ϊ9.6������F�˶���·�߳�Ϊ2.7cm��
��������
��1������CF������F��FH��CE���ӳ����ڵ�H����EH��FH��x��Ȼ�����tan��FCH��![]() ��
��![]() ��
��![]() ���������x��ֵ��
���������x��ֵ��
��2������������Ǻ����Ķ�������sin��CDA��![]() ��0��17���Ӷ����������D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6���������ݻ�����ʽ��������𰸣�
��0��17���Ӷ����������D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6���������ݻ�����ʽ��������𰸣�
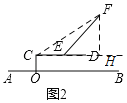
��1������CF������F��FH��CE���ӳ����ڵ�H����ͼ2��
�ߡ�FEH��45������FHC��90����
��EH��FH��x��
�ߡ�FCH��30����
��tan��FCH��![]() ��
��![]() ��
��![]() ��
��
��x��3![]() +3��
+3��
��CF��2x��6![]() +6��16��4cm��
+6��16��4cm��
��2����ʹ�ù����У�CD��AB�ļн�Ϊ��
sin��CDA��![]() ��0��17��
��0��17��
��sin9��6���0��17��
�൱��D���ڵ���AB��ʱ��CD��AB�ļн�Ϊ9��6����
�ߵ�F���˶�·������CΪԲ�ģ�CFΪ�뾶��Բ���ϣ�
�ҵ�D���ڵ���AB��ʱ����F�Ƶ�C��ת��9��6����
��l��![]() ��2��7cm��
��2��7cm��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�