题目内容
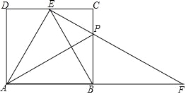
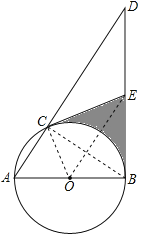
【题目】如图,AB为⊙O的直径,且AB=4,点C是弧AB上的一动点(不与A,B重合),过点B作⊙O的切线交AC的延长线于点D,点E是BD的中点,连接EC.
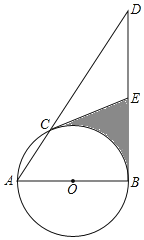
(1)若BD=8,求线段AC的长度;
(2)求证:EC是⊙O的切线;
(3)当∠D=30°时,求图中阴影部分面积.
【答案】(1)AC=![]() ;(2)见解析;(3)4
;(2)见解析;(3)4![]() ﹣
﹣![]()
【解析】
(1)连接BC,如图,连接BC,根据切线的性质得到∠ABD=90°,根据勾股定理得到AD=![]() =4
=4![]() ,根据三角形的面积公式和勾股定理即可得到结论;
,根据三角形的面积公式和勾股定理即可得到结论;
(2)连接OC,OE,由E是BD的中点,可得CE=BE,证明△OCE≌△OBE,得∠OCE=∠OBE=90°,则结论得证;
(3)阴影部分的面积即为四边形OBED的面积减去扇形COB的面积.
解:(1)如图,连接BC,
∵BD是⊙O的切线,
∴∠ABD=90°,
∵AB=4,BD=8,
∴AD=![]() =4
=4![]() ,
,
∵AB为⊙O的直径,
∴BC⊥AD,
∴BC=![]() =
=![]() =
=![]() ,
,
∴AC=![]() =
=![]() ;
;
(2)连接OC,OE,
∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△BDC中,
∵BE=ED,
∴DE=EC=BE,
∵OC=OB,OE=OE,
∴△OCE≌△OBE(SSS),
∴∠OCE=∠OBE,
∵BD是⊙O的切线,
∴∠ABD=90°,
∴∠OCE=∠ABD=90°,
∵OC为半径,
∴EC是⊙O的切线;
(3)∵OA=OB,BE=DE,
∴AD∥OE,
∴∠D=∠OEB,
∵∠D=30°,
∴∠OEB=30°,∠EOB=60°,
∴∠BOC=120°,
∵AB=4,
∴OB=2,
∴BE=2![]() .
.
∴四边形OBEC的面积为2S△OBE=2×![]() ×2×2
×2×2![]() =4
=4![]() ,
,
∴阴影部分面积为S四边形OBEC﹣S扇形BOC=4![]() ﹣
﹣![]() =4
=4![]() ﹣
﹣![]() .
.

【题目】在新冠病毒疫情防控期间,某校“停课不停学”,开展了网络教学.为了解九年级学生在网络学习期间英语学科和数学学科的学习情况,复课后从九年级学生中随机抽取60名学生进行了测试,获得了他们成绩(百分制)的数据,通过对成绩数据的整理、描述和分析,得到了如下部分信息.
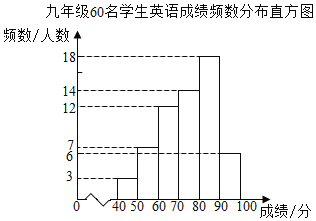
①英语成绩的频数分布直方图如图:
(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100.)
②英语和数学成绩的平均数、中位数、众数如表:
学科 | 平均数 | 中位数 | 众数 |
英语 | 74.8 | m | 83 |
数学 | 72.2 | 70 | 81 |
③英语成绩在70≤x<80这一组的数据是:
70 71 72 73 73 73 74 76 77 77 77 78 79 79
根据以上信息,回答下列问题:
(1)表中m的值是 .
(2)在此次测试中,李丽的英语成绩为74分,数学成绩为71分,该名学生成绩排名更靠前的学科是 .(填“英语”或“数学”),理由是 .
(3)若该校九年级共有500名学生,请你估计英语成绩超过77.5分的人数.