题目内容
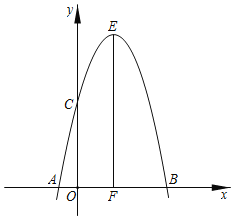
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x-3;(2)13.5;(3)存在,P1(-3,-3),P2(
x-3;(2)13.5;(3)存在,P1(-3,-3),P2(![]() ,3),P3(
,3),P3(![]() ,3).
,3).
【解析】
(1)根据OC=3OB,B(1,0),求出C点坐标(0,-3),把点B,C的坐标代入y=ax2+2ax+c,求出a点坐标即可求出函数解析式;
(2)过点D作DE∥y轴分别交线段AC于点E.设D(m,m2+2m-3),然后求出DE的表达式,把S四边形ABCD分解为S△ABC+S△ACD,转化为二次函数求最值;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.②平移直线AC交x轴于点E,交x轴上方的抛物线于点P2,P3,由题意可知点P2、P3的纵坐标为3,从而可求得其横坐标.
(1)∵B的坐标为(1,0),
∴OB=1.
∵OC=3OB=3,点C在x轴下方,
∴C(0,-3).
∵将B(1,0),C(0,-3)代入抛物线的解析式得:
![]() ,解得:a=
,解得:a=![]() ,C=-3,
,C=-3,
∴抛物线的解析式为y=![]() x-3.
x-3.
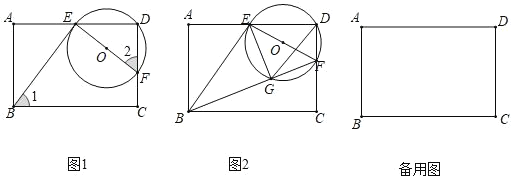
(2)如图1所示:过点D作DE∥y,交AC于点E.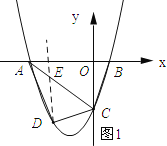
∵x=-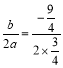 =-
=-![]() ,B(1,0),
,B(1,0),
∴A(-4,0).
∴AB=5.
∴S△ABC=![]() ABOC=
ABOC=![]() ×5×3=7.5.
×5×3=7.5.
设AC的解析式为y=kx+b.
∵将A(-4,0)、C(0,-3)代入得:
![]() ,解得:k=-
,解得:k=-![]() ,b=-3,
,b=-3,
∴直线AC的解析式为y=-![]() x-3.
x-3.
设D(a,![]() a2+
a2+![]() a-3),则E(a,-
a-3),则E(a,-![]() a-3).
a-3).
∵DE=-![]() (a+2)2+3,
(a+2)2+3,
∴当a=-2时,DE有最大值,最大值为3.
∴△ADC的最大面积=![]() DEAO=
DEAO=![]() ×3×4=6.
×3×4=6.
∴四边形ABCD的面积的最大值为13.5.
(3)存在.
①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.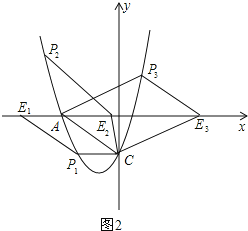
∵C(0,-3),令![]() x-3=-3,
x-3=-3,
∴x1=0,x2=-3.
∴P1(-3,-3).
②平移直线AC交x轴于点E2,E3,交x轴上方的抛物线于点P2,P3,当AC=P2E2时,四边形ACE2P2为平行四边形,当AC=P3E3时,四边形ACE3P3为平行四边形.
∵C(0,-3),
∴P2,P3的纵坐标均为3.
令y=3得:![]() x-3=3,解得;x1=
x-3=3,解得;x1=![]() ,x2=
,x2=![]() .
.
∴P2(![]() ,3),P3(
,3),P3(![]() ,3).
,3).
综上所述,存在3个点符合题意,坐标分别是:P1(-3,-3),P2(![]() ,3),P3(
,3),P3(![]() ,3).
,3).

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?