Question

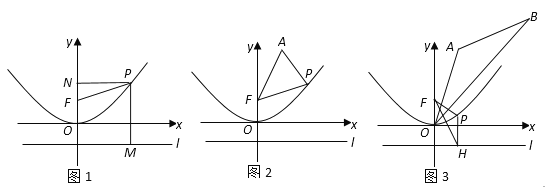
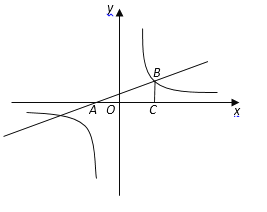
【题目】如图，平面直角坐标系中，直线与x轴交于点A，与双曲线在第一象限内交于点B，BC丄x轴于点C，OC=2AO．

（1）求双曲线的解析式．

（2）点D为y轴上一个动点，若S△ADB=3，求点D的坐标．

Answer 1

【答案】（1）y=；（2）(0，)或(0，)

【解析】

(1)先利用一次函数与图象的交点，再利用OC=2AO求得C点的坐标，然后代入一次函数求得点B的坐标，进一步求得反比例函数的解析式即可；

(2)先求得直线与y轴交于点E的坐标，设点D的坐标为(0，m)，得到DE=|m﹣|，利用S△ADB=S△ADE+S△BDE=3，即可求解．

(1)对于直线，

令，则，

∴直线与x轴交于点A的坐标为(﹣1，0)，

∴OA=1，

又∵OC=2OA，

∴OC=2，

∴点B的横坐标为2，

代入直线，得y=，

∴点B的坐标为(2，)．

∵点B在双曲线上，

∴2×=3，

∴双曲线的解析式为y=；

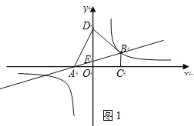
(2)如图1：

对于直线，

令，则，

∴直线与y轴交于点E的坐标为(0，)，

设点D的坐标为(0，m)，连接AD、BD，

∴DE=|m﹣|．

∵S△ADB=S△ADE+S△BDE=3，

∴×|m﹣|×(2+1)=3，

∴|m﹣|=2．

解得：=，．

∴点D的坐标为(0，)或(0，)．