题目内容
【题目】在世界经济的影响下,国家采取扩大内需的政策,基建投资成为拉动内需最强有力的引擎,金强公司中标一项工程,在甲、乙两地施工,其中甲地需推土机30台,乙地需推土机26台,公司在A、B两地分别库存推土机32台和24台,现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,设从A地运往甲地x台推土机,运这批推土机的总费用为y元.
(1)根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地(台) | 乙地(台) | 合计 | |
A地 | x | A地库存:32 (台) | |
B地 | B地库存:24 (台) | ||
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)求y与x的函数关系式;
(3)当x取何值时,能使运送这批推土机的总费用最少?
【答案】(1)见解析;(2)y=400x+12600;(3)当x=6时,总费用最小
【解析】
(1)设从A地运往甲地x台,从A地运往乙地的推土机(32x)台,从B地运往甲地的推土机(30x),运往乙地的推土机(x6)台,
(2)根据现从A地运一台到甲、乙两地的费用分别是400元和300元.从B地运一台到甲、乙两地的费用分别为200元和500元,可求出运这批推土机的总费用.
(2)根据函数的性质可判断费用何时最少.
解:(1) 根据题意,可将库存地和施工地之间推土机的运输数量列表如下:
甲地 | 乙地 | 合计 | |
A地 | x (台) | 32-x (台) | A地库存:32 (台) |
B地 | 30-x (台) | 26-(32-x)=24-(30-x)=x-6 (台) | B地库存:24 (台) |
合计 | 甲地需求:30 (台) | 乙地需求:26 (台) | 总计:56 (台) |
(2)从A地往甲地运推土机的费用为:400x,
从A地往乙地运推土机的费用为:300(32-x),
从B地往甲地运推土机的费用为:200(30-x),
从B地往乙地运推土机的费用为:500[26-(32-x)].
故运甲、乙两地所需的这批推土机的总费用y可以表示为:
y=400x+300(32-x)+200(30-x)+500[26-(32-x)]=400x+12600,
即y=400x+12600.
(2) 由于各地之间的运输数量均与x的取值有关. 从实际情况来看,x的取值必须保证各地之间的运输数量均为非负数. 因此,x的取值必须满足:
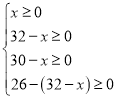 ,
,
解此不等式组,得
6≤x≤30.
由运送这批推土机的总费用y和从A地运往甲地的推土机的数量x的关系y=400x+12600可知,y与x满足一次函数关系,且y随x的增大而增大. 故要使总费用y最小,则x应取最小值.
又因为x的取值范围为:6≤x≤30,所以当x=6时,总费用最小.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案