题目内容
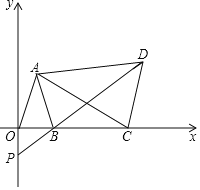
【题目】如图,在平面直角坐标系中,O为坐标原点.△ABC的边BC在x轴上,A、C两点的坐标分别为A(0,m)、C(n,0),B(﹣5,0),且![]() ,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
,点P从B出发,以每秒2个单位的速度沿射线BO匀速运动,设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连接PA,用含t的代数式表示△POA的面积;
(3)当P在线段BO上运动时,是否存在一点P,使△PAC是等腰三角形?若存在,请写出满足条件的所有P点的坐标并求t的值;若不存在,请说明理由。

【答案】(1)A的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)存在一点
;(3)存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.
【解析】
(1)根据偶次方和算术平方根的非负性得出![]() ,
,![]() ,求出即可;
,求出即可;
(2)分为三种情况:当![]() 时,
时,![]() 在线段
在线段![]() 上,②当
上,②当![]() 时,
时,![]() 和
和![]() 重合,③当
重合,③当![]() 时,
时,![]() 在射线
在射线![]() 上,求出
上,求出![]() 和
和![]() ,根据三角形的面积公式求出即可;
,根据三角形的面积公式求出即可;
(3)分为三种情况:①![]() 为顶角时,找出腰长关系便可解;②
为顶角时,找出腰长关系便可解;②![]() 为顶角时,找出腰长关系便可解;③
为顶角时,找出腰长关系便可解;③![]() 为顶角时,根据勾股定理可求得.
为顶角时,根据勾股定理可求得.
解:(1)![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ;
;
(2)![]() ,
,
![]() ,
,
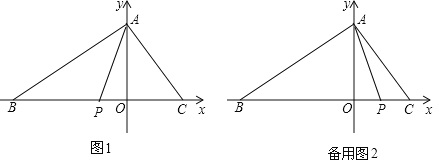
①当![]() 时,
时,![]() 在线段
在线段![]() 上,如图1,
上,如图1,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
②当![]() 时,
时,![]() 和
和![]() 重合,此时
重合,此时![]() 不存在,即
不存在,即![]() ;
;
③当![]() 时,
时,![]() 在射线
在射线![]() 上,如备用图2,
上,如备用图2,
![]() ,
,![]() ,
,
![]() 的面积
的面积![]() ;
;
(3)![]() 在线段
在线段![]() 上运动使
上运动使![]() 是等腰三角形,分三种情况,
是等腰三角形,分三种情况,
①![]() 为顶角时,即
为顶角时,即![]() ,
,
![]() 为
为![]() 中垂线,
中垂线,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() .
.
![]() ;
;
②![]() 为顶角时,
为顶角时,![]()
根据勾股定理可得,![]() ,
,
∵P在OB上,
![]() 点坐标为
点坐标为![]() ,
,![]()
![]() ;
;
③![]() 为顶角时,
为顶角时,![]() ,设
,设![]() ,
,
根据勾股定理,在![]() 中,
中,![]()
解得![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
综上,存在一点![]() 、
、![]() 、
、![]() ,
,![]() 相对应的时间分别是
相对应的时间分别是![]() 、1.5、
、1.5、![]() 使
使![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目