��Ŀ����
����Ŀ����ͼ�����κ���y=![]() x2��6
x2��6![]() x+5
x+5![]() ��ͼ��x����A��B���㣬��y���ڵ�C������BC��
��ͼ��x����A��B���㣬��y���ڵ�C������BC��
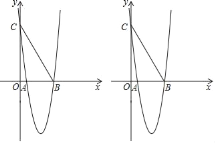
��1��ֱ��д����B��C�����꣬B������C������
��2����P��y���Ҳ��������ϵ�һ�㣬����PB��PC������PBC�����15![]() �����P�����꣮
�����P�����꣮
��3����EΪ�߶�BC��һ�㣨�����˵㣩������AE��һ����M�ӵ�A���������߶�AE��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�EC��ÿ��2����λ���ٶ��˶���C��ֹͣ������E������������ʱ����M�������˶�����ʱ���٣�������ʱ�������룮
��4������Q��y���ϣ�����AQBȡ�����ֵʱ��ֱ��д����Q������������
���𰸡���1����0��5![]() ������5��0��;��2��P������Ϊ����2����3 ������3����4 ��������1��10 ����6��5 ��;��3����4��
������5��0��;��2��P����������2����3 ������3����4 ��������1��10 ����6��5 ��;��3����4��![]() ����(2
����(2![]() +1);��4����3��
+1);��4����3��![]() ��.
��.
��������
��1����x��0��y��0�ֱ����y=![]() x2��6
x2��6![]() x+5
x+5![]() ���������B��C�����ꣻ��2����x���ϵ�D��ʹ����DBC�����15
���������B��C�����ꣻ��2����x���ϵ�D��ʹ����DBC�����15![]() �����BD�ij�������ֱ��BC�Ľ���ʽ���õ�D������Ϊ����1��0����11��0������������D����Ϊ����1��0���루11��0������������ݹ���Dƽ����BC��ֱ��l�������߽���Ϊ����������P�����������������P������ꣻ��3������֪����AE���ʱ��M��ʱ���٣���AE��BC�ڵ�Eʱ��AE��̣��������Ǻ������AE��EB�ij����������E��������Լ�M���˶�������ʱ�䣻��4����AB��Ϊ����Բ��Բ��F��x���Ϸ�����Բ�뾶Խ��x���Ϸ��ĵ���AB�������н�Խ��
�����BD�ij�������ֱ��BC�Ľ���ʽ���õ�D������Ϊ����1��0����11��0������������D����Ϊ����1��0���루11��0������������ݹ���Dƽ����BC��ֱ��l�������߽���Ϊ����������P�����������������P������ꣻ��3������֪����AE���ʱ��M��ʱ���٣���AE��BC�ڵ�Eʱ��AE��̣��������Ǻ������AE��EB�ij����������E��������Լ�M���˶�������ʱ�䣻��4����AB��Ϊ����Բ��Բ��F��x���Ϸ�����Բ�뾶Խ��x���Ϸ��ĵ���AB�������н�Խ��
��ԲF��y�����ڵ�Qʱ����AQBȡ�����ֵ����ͼ����FA��FB��FQ����FH��AB�ڵ�H�����QF��FH�ij���������õ�Q����.
�⣺��1����x=0ʱ��y=5![]()
��y=0ʱ�� ![]() x2��6
x2��6![]() x+5
x+5![]() =0
=0
���
x1=1��x2=5
�ʴ�Ϊ����0��5![]() ������5��0��
������5��0��
��2����x���ϵ�D��ʹ����DBC�����15![]() .
.
��![]() BDOC��15
BDOC��15![]() ��
��
���BD=6
��C��0��5![]() ����B��5��0��
����B��5��0��
�����ֱ��BC����ʽΪ��y=��![]() x��5
x��5![]() x
x
�ʵ�D����Ϊ����1��0����11��0��
��D����Ϊ����1��0��ʱ������Dƽ����BC��ֱ��l�������߽���Ϊ����������P
������ֱ��l�Ľ���ʽΪ��y=��![]() x��
x��![]()
��ֱ��l�������߽���ã�
![]() x2��6
x2��6![]() x+5
x+5![]() =��
=��![]() x��
x��![]()
���
x1=2��x2=3
��P��������2����3![]() ����3����4
����3����4![]() ��
��
ͬ������D����Ϊ��11��0��ʱ��ֱ��l�Ľ���ʽΪy=��![]() x��11
x��11![]()
��ֱ��l�������߽���ã�
![]() x2��6
x2��6![]() x+5
x+5![]() =��
=��![]() x��11
x��11![]()
���
x1=��1��x2=6
���P��������1��10![]() ������6��5
������6��5![]() ��
��
������������P����������2����3![]() ������3����4
������3����4![]() ��������1��10
��������1��10![]() ����6��5
����6��5![]() ��
��
��3������֪����AE���ʱ��M��ʱ����
��AE��BC�ڵ�E������֪����ABC=60�㣬AB=4
��AE=2![]() ��EB=2
��EB=2
���E����Ϊ��4��![]() ������M�������˶�����ʱ����Ϊ��2
������M�������˶�����ʱ����Ϊ��2![]() ��1����
��1����
�ʴ�Ϊ����4��![]() ������2
������2![]() ��1��
��1��
��4����AB��Ϊ����Բ��Բ��F��x���Ϸ�����Բ�뾶Խ��x���Ϸ��ĵ���AB�������н�Խ��
��ԲF��y�����ڵ�Qʱ����AQBȡ�����ֵ��
��ͼ����FA��FB��FQ����FH��AB�ڵ�H
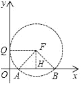
���֪AH=2
��QF=OH=3
��FH=![]() ��
��![]()
���Q������3��![]() ��
��
�ʴ�Ϊ����3��![]() ��
��

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�