题目内容
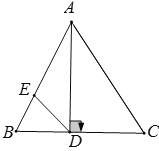
【题目】如图所示,在△ABC中,已知AD⊥BC,∠B=64°,∠C=56°,
(1)求∠BAD和∠DAC的度数;
(2)若DE平分∠ADB,求∠AED的度数.
【答案】(1)34°(2)109°
【解析】
(1)在Rt△BAD和Rt△BAD中,根据直角三角形的两个锐角互余分别求解即可得;
(2)由DE平分∠ADB,AD⊥BC求得∠BDE=45°,再根据三角形外角的性质求解即可.
(1)∵AD⊥BC,
∴在Rt△BAD中,∠BAD+∠B=90°,
又∵∠B=64°,∴∠BAD=26°;
∴在Rt△BAD中,∠DAC+∠C=90°,
又∵∠C=56°,∴∠DAC=34°;
(2)∵AD⊥BC,DE平分∠ADB,∴∠BDE=45°,
在△BED中,∠B=64°,∴∠B+∠BDE=109°,
∵∠AED=∠B+∠BDE,
∴∠AED=109°.

练习册系列答案
相关题目