题目内容

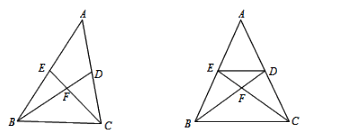
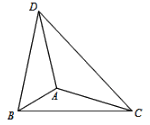
【题目】如图，△ABC中，∠ABC=30，BC=4，AB=，将边AC绕着点A逆时针旋转120得到AD，则BD的长为_______________．

【答案】．

【解析】

如图，将AB绕点A顺时针旋转120°至接EA,EC，过A作AM⊥BE于M点，过E作 EF⊥BC于点F，易证△EAC≌△BAD，则BD=EC，根据题意可得，E、 A、F三点共线，并求得BF,EF,CF的值，最后用勾股定理求得EC即可完成解答．

解:如图: 将AB绕点A顺时针旋转120°至接EA,EC，过A作AM⊥BE于M点，过A作 AF⊥BC于点F

∴∠BAE=∠DAC

∴∠BAD=∠EAC

又∵AE=BA,AC=AD

∴△EAC≌△BAD(SAS)

∴BD=EC

∵∠ABC=30， AB=

∴AF=,AE=,FC=

∵∠ABC=30,AF⊥BC

∴∠BAF=60

∵∠BAF=120

∴E、 A、F三点共线，

∴EF=AE+AF=

∴BD=EC=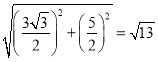

故答案为．

练习册系列答案
相关题目

【题目】如图，平行四边形ABCD，E、F两点在对角线BD上，且BE＝DF，连接AE，EC，CF，FA．

（1）求证：四边形AECF是平行四边形．

（2）若AF＝EF，∠BAF＝108°，∠CDF＝36°，直接写出图中所有与AE相等的线段（除AE外）．

【题目】如图①，在菱形ABCD中，动点P从点B出发，沿折线B→C→D→B运动．设点P经过的路程为x，△ABP的面积为y．把y看作x的函数，函数的图象如图②所示，则图②中的b等于（　　）

A. B. C. 5D. 4

【题目】如图，直线与x轴交于点B，与y轴交于点C，抛物线经过B、C两点，且与x轴交于另一点A．

（1）求抛物线的解析式．

（2）点P是线段BC下方的抛物线上的动点（不与点B、C重合），过P作PD∥y轴交BC于点D，以PD为直径的圆交BC于另一点E，求DE的最大值及此时点P的坐标；

（3）当（2）中的DE取最大值时，将△PDE绕点D旋转，当点P落在坐标轴上时，求点E的坐标．

【题目】综合与实践

情景再现

我们动手操作：把正方形ABCD，从对角线剪开就分剪出两个等腰直角三角形，把其中一个等腰三角形与正方形ABCD重新组合在一起，图形变得丰富起来，当图形旋转时问题也随旋转应运而生．

如图①把正方形ABCD沿对角线剪开，得两个等腰直角三角形△ACD和△BCE，

（1）问题呈现

我们把剪下的两个三角形一个放大另一个缩小拼成如图②所示

①点P是一动点，若AB=3，PA=1，当点P位于_ __时，线段PB的值最小；若AB=3，PA=5，当点P位于__ _时，线段PB有最大值．PB的最大值和最小值分别是______．

②直接写出线段AE与DB的关系是_ ________．

（2）我们把剪下的其中一个三角形放大与正方形组合如图③所示，点E在直线BC上，FM⊥CD交直线CD于M．

①当点E在BC上时，通过观察、思考易证：AD=MF+CE；

②当点E在BC的延长线时，如图④所示；

当点E在CB的延长线上时，如图⑤所示，

线段AD、MF、CE具有怎样的数量关系？写出你的猜想，并选择图④或图⑤证明你的猜想．

问题拓展

（3）连接EM，当=8，=50，其他条件不变，直接写出线段CE的长_______．

【题目】如图，△ABC的两条中线BD、CE交于点F．

（1） = _______；

（2）若BE2 = EFEC，且 = ，EF =，求DE的长；

【题目】如图，正方形 ABCD 和正三角形 AEF 都内接于⊙O，EF 与 BC，CD 分别相交于点 G，H，则 的值为（ ）

A.B.C.D.2

【题目】如图，已知△ABC的顶点坐标分别为A(3，0)，B(0，4)，C(-3，0)，动点M，N同时从A点出发，N沿A→C，M沿折线A→B→C，均以每秒1个单位长度的速度移动，当一个动点到达终点C时，另一个动点也随之停止移动，移动时间记为t秒．连接MN．

（1）移动过程中，将△ABC沿直线MN折叠，若点A恰好落在BC边上的点D处，求此时t的值．

（2）当点M，N移动时，记△ABC在直线MN右侧部分的面积为S，求S关于时间t的函数关系式．

【题目】甲、乙两车分别从A、B两地同时出发相向而行，并以各自的速度匀速行驶，两车在相遇之前同时改变了一次速度，并同时到达各自目的地，两车距B地的路程y（km）与出发时间x（h）之间的函数图象如图所示．

（1）分别求甲、乙两车改变速度后y与x之间的函数关系式；

（2）若m＝1，分别求甲、乙两车改变速度之前的速度；

（3）如果两车改变速度时两车相距90km，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网