题目内容
【题目】综合与实践
情景再现
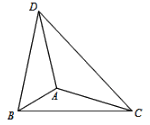
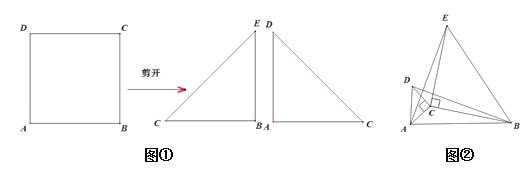
我们动手操作：把正方形ABCD，从对角线剪开就分剪出两个等腰直角三角形，把其中一个等腰三角形与正方形ABCD重新组合在一起，图形变得丰富起来，当图形旋转时问题也随旋转应运而生．
如图①把正方形ABCD沿对角线剪开，得两个等腰直角三角形△ACD和△BCE，
（1）问题呈现
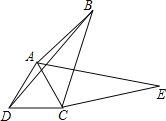
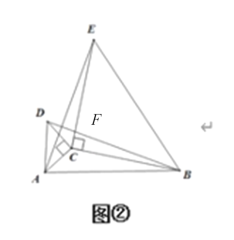
我们把剪下的两个三角形一个放大另一个缩小拼成如图②所示
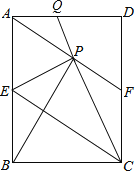
①点P是一动点，若AB=3，PA=1，当点P位于_ __时，线段PB的值最小；若AB=3，PA=5，当点P位于__ _时，线段PB有最大值．PB的最大值和最小值分别是______．
②直接写出线段AE与DB的关系是_ ________．
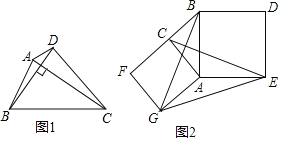
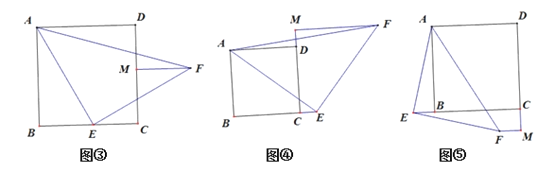
（2）我们把剪下的其中一个三角形放大与正方形组合如图③所示，点E在直线BC上，FM⊥CD交直线CD于M．
①当点E在BC上时，通过观察、思考易证：AD=MF+CE；
②当点E在BC的延长线时，如图④所示；
当点E在CB的延长线上时，如图⑤所示，
线段AD、MF、CE具有怎样的数量关系？写出你的猜想，并选择图④或图⑤证明你的猜想．
问题拓展
（3）连接EM，当
=8，
=50，其他条件不变，直接写出线段CE的长_______．
【答案】（1）①AB，BA延长线，最大值是8，最小值是2；；②AE=BD，AE⊥BD；
（2）选择图④，则AD+CE=MF.见详解；
（3）1或7.
【解析】
（1）①P为一动点，PA=1，则点P在以A为圆心，以1为半径圆上，画图的解；同理PA=5，则点P在以A为圆心，以5为半径圆上，问题得解；②△ACE≌△DCB，问题得解；
（2）类比①；通过添加辅助线FG⊥BE，交BE延长线于G，证明△ABE≌△EGF，进行线段转移，得出结论；
（3）已知
=8，通过三角形面积公式，求出CF=4，△AEF为等腰直角三角形，
=50，得出EF=5，勾股定理得EG=3，计算得出结果.
解：（1）①AB；BA延长线；最大值是8，最小值是2；
②AE=BD，AE⊥BD；
证明：如图，∵△ACD和△BCE都是等腰直角三角形，
∴AC=DC，EC=BC，∠ACD=∠BCE=90°，
∴∠ACD+∠DCE=∠DCE+∠BCE，
即：∠ACE=∠DCB，
∴△ACE≌△DCB，
∴AE=BD，∠AEC=∠DBC，
∵∠BFC+∠DBC=90°，∠BFC=∠EFD,
∴∠AEC+∠EFD=90°
∴AE⊥BD
（2）②答：选择图④，则AD+CE=MF.
证明：如图，作FG⊥BE，交BE延长线于G，
∵四边形ABCD是正方形，
∴∠B=∠MCG=∠G==90°，AD=AB=BC，
∴∠BAE+∠AEB=90°.
∵△AEF为等腰直角三角形，
∴AE=EF，∠AEF=90°，
∴∠AEB+∠GEF=90°，
∴∠BAE=∠GEF，
∴△ABE≌△EGF，
∴AB=EG
∵ AB=BC，
∴EG=BC，
∴EG+CE=BC+CE，
即：CG=BC+CE=AD+CE.
∵∠G=∠MCG=90°，FM⊥CD，
∴四边形CMFG为矩形，
∴MF=CG，
∴AD+CE=MF
（3）∵CG=BC+CE=FG，四边形CMFG为矩形，
∴四边形CMFG为正方形，
∵
，
∴
∴FG=4
∵=50，△AEF为等腰直角三角形，
∴EF=5,
∴在直角△EFG中，EG=3，
∴CE=CG-EG=4-3=1或CE=CG+EG=4+3=7 .
