题目内容
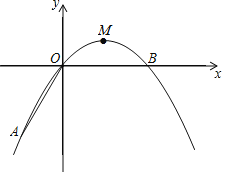
【题目】如图,直线![]() 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线![]() 经过B、C两点,且与x轴交于另一点A.
经过B、C两点,且与x轴交于另一点A.
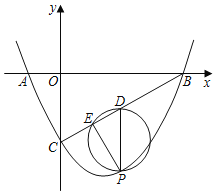
(1)求抛物线的解析式.
(2)点P是线段BC下方的抛物线上的动点(不与点B、C重合),过P作PD∥y轴交BC于点D,以PD为直径的圆交BC于另一点E,求DE的最大值及此时点P的坐标;
(3)当(2)中的DE取最大值时,将△PDE绕点D旋转,当点P落在坐标轴上时,求点E的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)m=2时,DE有最大值
x﹣2;(2)m=2时,DE有最大值![]() ,此时P
,此时P![]() ;(3)
;(3)![]() ,或E
,或E![]() 或
或![]()
【解析】
(1)求出![]() ,
,![]() ,将
,将![]() 与
与![]() 代入抛物线解析式即可求出
代入抛物线解析式即可求出![]() 、
、![]() 的值,进而确定函数解析式;
的值,进而确定函数解析式;
(2)设![]() ,可得
,可得![]() ,利用P、D的坐标表示出PD,再由点到直线距离公式求得线段PE的代数式,根据勾股定理求得线段DE的代数式,通过整理即可得到当
,利用P、D的坐标表示出PD,再由点到直线距离公式求得线段PE的代数式,根据勾股定理求得线段DE的代数式,通过整理即可得到当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时
,此时![]() ;
;
(3)当点P落在坐标轴上时,先求出P点坐标,再分三种情况讨论:①当![]() 时;②当
时;②当![]() ;③
;③![]() ;分别求出
;分别求出![]() 点坐标即可.
点坐标即可.
解:(1)在直线![]() 中,
中,
当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
将![]() ,
,![]() 分别代入
分别代入![]() 得:
得:
![]() ,
,
解得: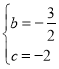 ,
,
![]() ;
;
(2)设![]() ,
,
![]() 是线段
是线段![]() 下方,
下方,
![]() ,
,
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 轴与
轴与![]() 交于点
交于点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,则PE为点P到直线BC:
,则PE为点P到直线BC:![]() 的距离,
的距离,
∴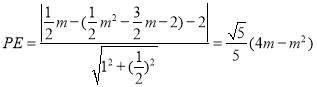 ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时
,此时![]() ;
;
(3)由(2)可知,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
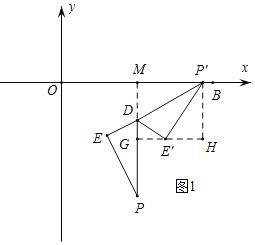
①如图1,当P点落在如图所示的位置,即![]() ,延长
,延长![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ;
;
![]() ,
,
∴∠DE'G+∠E'DG=∠DE'G+∠P' E'H=90°,
∴∠E'DG=∠P' E'H,
∴△DGE'∽△E'HP',
![]()
![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
整理得: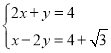 ,解得:
,解得: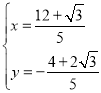 ,
,
∴![]() ;
;
②如图2,![]() 与
与![]() 关于
关于![]() 对称,
对称,
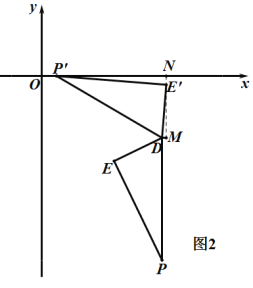
∴![]() ,
,
过点![]() 作
作![]() 轴垂线
轴垂线![]() ,过点D作DM⊥
,过点D作DM⊥![]() 交
交![]() 的延长线于点M,
的延长线于点M,
同理①得:△DME'∽△E'NP',
∴![]() ,
,
![]()
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
整理得: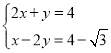 ,解得:
,解得: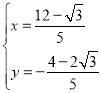 ,
,
∴![]() ;
;
③如图3,![]() 在y轴上,
在y轴上,
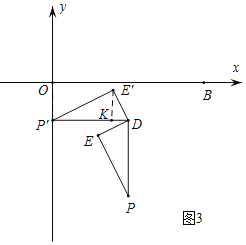
∵![]() ,
,
![]() ,
,
![]() ,
,
过点![]() 作
作![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() △
△![]() 中,
中,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ;
;
综上所述:当点P落在坐标轴上时,点E的坐标为![]() 或
或![]() 或
或![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案