题目内容
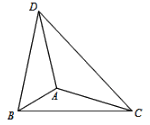
【题目】如图，△ABC的两条中线BD、CE交于点F．
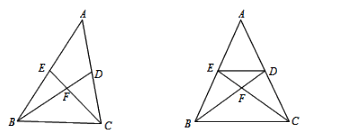
（1）
= _______；
（2）若BE2 = EFEC，且
= 
，EF =
，求DE的长；
【答案】（1）
；（2）2
．
【解析】
(1)由BD、CE为△ABC的两条中线,则ED∥BC,ED=BC,则△EFD∽△CFB,则
即可完成解答．
(2)由(1)得,由EF=,则FC=2,EC=3;又由BE2 = EFEC得
,结合∠BEF=∠BEF,证得△BEF∽△ECB,可知
,进而求得DE；
解：（1）∵BD、CE为△ABC的两条中线
∴ED∥BC,ED=BC
∴△EFD∽△CFB
∴，
故答案为；
（2）∵EF=
∴FC=2,EC=3
又∵BE2 = EFEC=18
∴,BE=3
,BF=2DF=4
又∵∠BEF=∠BEF
∴△BEF∽△ECB(两边对应成比例且夹角相等的三角形相似)
∴
∴BC=4, ED=BC=2
．
练习册系列答案
相关题目
