Question

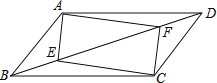
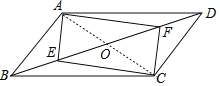
【题目】如图，平行四边形ABCD，E、F两点在对角线BD上，且BE＝DF，连接AE，EC，CF，FA．

（1）求证：四边形AECF是平行四边形．

（2）若AF＝EF，∠BAF＝108°，∠CDF＝36°，直接写出图中所有与AE相等的线段（除AE外）．

Answer 1

【答案】（1）证明见解析；（2）BE、CF、DF．

【解析】

（1）连接AC交BD于点O，根据平行四边形的对角线互相平分可得OA＝OC，OB＝OD，然后求出OE＝OF，再根据对角线互相平分的四边形是平行四边形即可证明；

（2）根据平行线的性质得到∠ABF＝∠CDF＝36°，根据三角形的内角和得到∠AFB＝180°﹣108°﹣36°＝36°，即可得到结论．

（1）证明：如图，连接AC交BD于点O，

在平行四边形ABCD中，OA＝OC，OB＝OD，

∵BE＝DF，

∴OB﹣BE＝OD﹣DF，

即OE＝OF，

∴四边形AECF是平行四边形（对角线互相平分的四边形是平行四边形；

（2）解：∵AB∥CD，

∴∠ABF＝∠CDF＝36°，

∵AF＝EF，

∴∠FAE＝∠FEA＝72°，

∵∠AEF＝∠EBA+∠EAB，

∴∠EBA＝∠EAB＝36°，

∴EA＝EB，

同理可证CF＝DF，

∵AE＝CF，

∴与AE相等的线段有BE、CF、DF．