题目内容
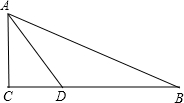
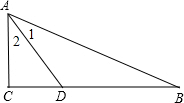
已知：如图，在△ABC中，∠C=90°，∠B=30°，AD是∠BAC的平分线，且AB=4
，求：AD的长及S△ADB．
| 3 |
∵∠C=90°，∠B=30°，
∴∠BAC=60°，
∵AB=4
，
∴AC=
AB=
×4
=2
，
∵AD平分∠BAC，
∴∠1=∠2=30°，
∴∠1=∠B，
在Rt△ACD中，cos∠2=
，
∴AD=
=
=4；
∵∠1=∠B，
∴BD=AD=4，
∴S△ABD=
BD•AC=
×4×2
=4
，
∴AD的长为4，△ABD的面积为4
．
∴∠BAC=60°，
∵AB=4
| 3 |
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵AD平分∠BAC，
∴∠1=∠2=30°，
∴∠1=∠B，
在Rt△ACD中，cos∠2=
| AC |
| AD |
∴AD=
| AC |
| cos∠2 |
2
| ||||
|
∵∠1=∠B，
∴BD=AD=4，
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴AD的长为4，△ABD的面积为4
| 3 |
练习册系列答案
出彩同步大试卷系列答案
相关题目
