题目内容
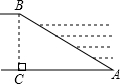
已知：如图，楼顶有一根天线，为了测量楼的高度，在地面上取成一条直线的三点E、D、C，在点C处测得天线顶端A的仰角为60°，从点C走到点D，CD=6米，从点D处测得天线下端B的仰角为45°．又知A、B、E在一条线上，AB=25米，求楼高BE．
∵从点D处测得天线下端B的仰角为45°，
∴DE=BE．
设BE=x米，则
∴AE=（x+25）米，CE=（x+6）米，
∵在点C处测得天线顶端A的仰角为60°，
∴tanC=
，
∴
=
，
∴x=
×（7+19
），
即楼高BE=
×（7+19
）米．
∴DE=BE．
设BE=x米，则
∴AE=（x+25）米，CE=（x+6）米，
∵在点C处测得天线顶端A的仰角为60°，
∴tanC=
| AE |
| CE |
∴
| x+25 |
| x+6 |
| 3 |
∴x=
| 1 |
| 2 |
| 3 |
即楼高BE=
| 1 |
| 2 |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
其中一个门的门前台阶改造成供轮椅行走的斜坡，并且设计斜坡的倾斜角为9度．请计算从斜坡起点A到台阶前的点B的水平距离．
