题目内容
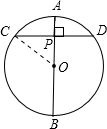
如图,在⊙O中,直径AB垂直于弦CD,垂足为P。若PA=1,PB=4,则CD的长为


A. | B.2 | C.4 | D. |
C
分析:首先由PA=1,PB=4,求得直径AB的值,继而求得PO与OC的值,然后利用垂径定理,求得PC的值,即可求得CD的长.
解答:解:连接OC.
∵PA=1,PB=4,
∴AB=PA+PB=5,
∴OA=OC=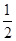 AB=
AB=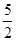 ,PO=OA-PA=
,PO=OA-PA=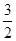 ,
,
∵在⊙O中,直径AB⊥弦CD,
∴CD=2PC,
∴在Rt△POC中,PC= =
=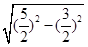 =2,
=2,
∴CD=2PC=4.
故选C.
解答:解:连接OC.

∵PA=1,PB=4,
∴AB=PA+PB=5,
∴OA=OC=
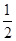 AB=
AB=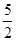 ,PO=OA-PA=
,PO=OA-PA=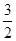 ,
,∵在⊙O中,直径AB⊥弦CD,
∴CD=2PC,
∴在Rt△POC中,PC=
 =
=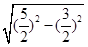 =2,
=2,∴CD=2PC=4.
故选C.

练习册系列答案
相关题目
 的度数
的度数
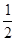 ,求⊙O的直径.
,求⊙O的直径.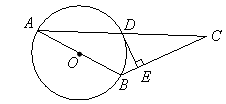

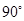 ,OA=OB=
,OA=OB=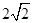 ,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.
,以点O为圆心的圆与AB相切于点C,则图中阴影部分的面积是______________.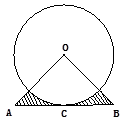
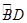 ,则图中阴影部分的面积是_________.
,则图中阴影部分的面积是_________.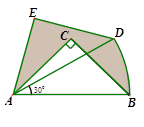
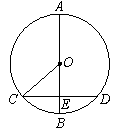
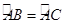 ; ②
; ②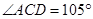 ; ③
; ③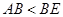 ; ④△AEC∽△ACD.
; ④△AEC∽△ACD.