题目内容
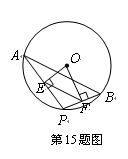
、已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
小题1:求证:DE为⊙O的切线;
小题2:若DE=2,tanC=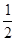 ,求⊙O的直径.
,求⊙O的直径.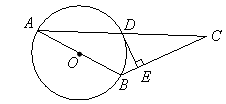
小题1:求证:DE为⊙O的切线;
小题2:若DE=2,tanC=
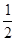 ,求⊙O的直径.
,求⊙O的直径.
小题1:证明:联结OD. ∵D为AC中点, O为AB中点,
∴OD为△ABC的中位线. ∴OD∥BC.
∵DE⊥BC, ∴∠DEC=90°.
∴∠ODE=∠DEC=90°. ∴OD⊥DE于点D.
∴DE为⊙O的切线.
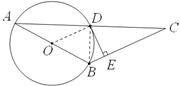
小题2:解:联结DB.∵AB为⊙O的直径,
∴∠ADB=90°.∴DB⊥AC.∴∠CDB=90°.
∵D为AC中点, ∴AB=AC.
在Rt△DEC中,∵DE="2" ,tanC=
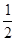 , ∴EC=
, ∴EC=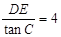 .
. 由勾股定理得:DC=
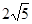 .
.在Rt△DCB 中, BD=
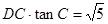 .由勾股定理得: BC=5.
.由勾股定理得: BC=5.∴AB= BC=5.
∴⊙O的直径为5.
略

练习册系列答案
相关题目
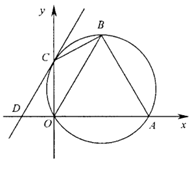
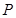 在第一象限,⊙
在第一象限,⊙ 轴相切于点
轴相切于点 ,与
,与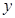 轴交于
轴交于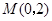 ,
, 两点,则点
两点,则点