题目内容
如图,A、B、C是⊙O的圆周上三点,∠ACB=40°, 则∠ABO等于 度.

50
分析:已知A、B、C是⊙O上三点,∠ACB=40°,则OA=OB,即△OAB是等腰三角形,∠OAB=∠OBA,因为同弧所对的圆周角等于同弧所对的圆心角的一半,所以∠AOB=2∠ACB=2×40°=80°,那么∠ABO=(180°-∠AOB)÷2=50°.
解:∵∠ACB=40°,
∴∠AOB=2∠ACB=2×40°=80°,
又∵OA=OB,
∴∠ABO=(180°-∠AOB)÷2=50°.

练习册系列答案
相关题目
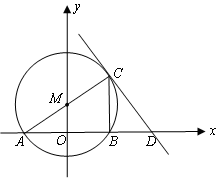
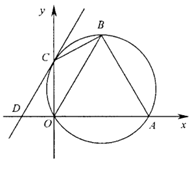
 在第一象限,⊙
在第一象限,⊙ 轴相切于点
轴相切于点 ,与
,与 轴交于
轴交于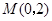 ,
, 两点,则点
两点,则点
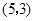
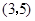

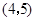
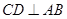 于
于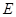 ,若
,若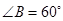 ,则
,则 度.
度.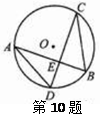



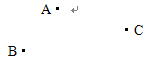
 是圆O的一条弦,
是圆O的一条弦, ,垂足为
,垂足为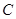 ,交圆O于点
,交圆O于点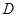 ,点
,点 在圆O上.(1)若
在圆O上.(1)若 ,求
,求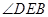 的度数;
的度数;
 ,
, ,求
,求