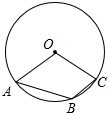
题目内容
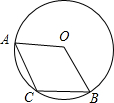
如图所示,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D点,OC交AB于E点.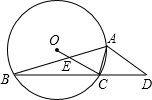
(1)求∠D的度数;
(2)求证:AC2=AD•CE.

(1)求∠D的度数;
(2)求证:AC2=AD•CE.
(1)连接OA,如图所示:
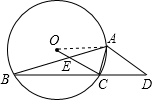
∵圆周角∠ABC与圆心角∠AOC所对的弧都为
,
∴∠AOC=2∠ABC,又∠ABC=15°,
∴∠AOC=30°,
又OA=OC,∴∠OAC=∠OCA=
=75°,
又∠BAC=45°,∠ABC=15°,
∴∠ACB=120°,
∴∠OCB=∠ACB-∠ACO=120°-75°=45°,
又OC∥AD,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,
又∠ACB=120°∴∠ACD=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,又∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴
=
,即AC2=AD•CE.

∵圆周角∠ABC与圆心角∠AOC所对的弧都为
 |
| AC |
∴∠AOC=2∠ABC,又∠ABC=15°,
∴∠AOC=30°,
又OA=OC,∴∠OAC=∠OCA=
| 180°-30° |
| 2 |
又∠BAC=45°,∠ABC=15°,
∴∠ACB=120°,
∴∠OCB=∠ACB-∠ACO=120°-75°=45°,
又OC∥AD,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,
又∠ACB=120°∴∠ACD=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,又∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴
| AC |
| AD |
| CE |
| AC |

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目