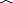题目内容
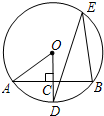
如图：
=
，D、E分别是半径OA和OB的中点，
求证：CD=CE．
 |
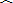| AC |
|
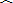| CB |
求证：CD=CE．
证明：连接OC．
在⊙O中，∵
=
∴∠AOC=∠BOC，
∵OA=OB，D、E分别是半径OA和OB的中点，
∴OD=OE，
∵OC=OC（公共边），
∴△COD≌△COE（SAS），
∴CD=CE（全等三角形的对应边相等）．
在⊙O中，∵
|
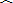| AC |
|
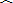| CB |
∴∠AOC=∠BOC，
∵OA=OB，D、E分别是半径OA和OB的中点，
∴OD=OE，
∵OC=OC（公共边），
∴△COD≌△COE（SAS），
∴CD=CE（全等三角形的对应边相等）．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
