题目内容
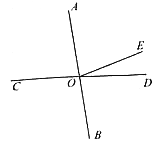
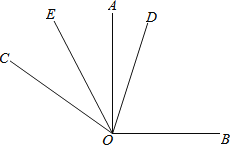
【题目】如图,已知同一平面内∠AOB=90°,∠AOC=60°.
(1)问题发现:∠BOD的余角是 ,∠BOC的度数是 ;
(2)拓展探究:若OD平分∠BOC,OE平分∠AOC,则∠DOE的度数是 ;
(3)类比延伸:在(2)条件下,如果将题目中的∠AOB=90°改为∠AOB=2∠β;∠AOC=60°改为∠AOC=2α(α<45°),其他条件不变,你能求出∠DOE吗?若能,请你写出求解过程:若不能,请说明理由.
【答案】(1)∠AOD,150°;(2)45°;(3)∠DOE=β,理由详见解析.
【解析】
(1)直接根据余角的定义得到∠BOD的余角,利用∠BOC=∠AOB+∠AOC求出即可;
(2)利用角平分线的性质和(1)中所求得出答案即可;
(3)根据角平分线的性质求出即可.
(1)∵∠AOB=90°,
∴∠AOD+∠BOD=90°,
∴∠BOD的余角是∠AOD,
∵∠AOC=60°,
∴∠BOC=∠AOB+∠AOC=90°+60°=150°,
故答案为:∠AOD,150°;
(2)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=![]() ∠BOC=75°,∠COE=
∠BOC=75°,∠COE=![]() ∠AOC=30°,
∠AOC=30°,
∴∠DOE的度数为:∠COD﹣∠COE=45°;
故答案为:45°;
(3)∵∠AOB=2β°,∠AOC=2α,
∴∠BOC=2β+2α,
∵OD、OE平分∠BOC,∠AOC,
∴∠DOC=![]() ∠BOC=β+α,∠COE=
∠BOC=β+α,∠COE=![]() ∠AOC=α,
∠AOC=α,
∴∠DOE=∠COD﹣∠COE=β+α﹣α=β.

练习册系列答案
相关题目