题目内容
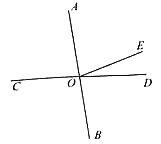
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
【答案】(1)∠AOE=80°;(2)∠AOD、∠BOC、∠BOE;(3),∠BOP的度数为130°或30°.
【解析】
(1)根据余角的定义及题意可得∠DOE=100°-∠AOE,再由∠AOE=4∠DOE即可求得∠AOE的度数;(2)根据补角的定义可得∠AOC+∠AOD=180°,∠AOC+∠BOC=180°,根据已知条件及(1)的结论可证得∠AOC+∠BOE=180°,即可得∠AOC的补角有∠AOD、∠BOC、∠BOE;(3)根据已知条件求得∠COP=130°, ∠DOP=50°,再分OP在直线CD上方和下方两种情况求解即可.
(1)∵∠AOE的余角比∠DOE小10°,
∴90°-∠AOE=∠DOE-10°,
∴∠DOE=100°-∠AOE
∵∠AOE=4∠DOE,
∴∠AOE=4(100°-∠AOE)
∴∠AOE=80°,
即:∠AOE的度数为80°;
(2)由题意可知:∠AOC+∠AOD=180°,∠AOC+∠BOC=180°,
∴∠AOC的补角有:∠AOD、∠BOC;
∵∠AOE=4∠DOE,∠AOE=80°,
∴∠DOE=20°,
∴∠AOD=∠AOE+∠DOE=100°,
∴∠BOD=∠AOC =80°,
∴∠BOE=∠BOD+∠DOE=80°+20°=100°,
∴∠AOC+∠BOE=80°+100°=180°.
∴∠BOE是∠AOC的补角.
综上,∠AOC的补角有:∠AOD、∠BOC、∠BOE;
(3)由(1)可得∠AOE=80°,∠DOE=![]() ∠AOE =20°,
∠AOE =20°,
∴∠AOD=∠AOE+∠DOE=100°,∠BOD=180°-∠A OD=80°,
∵∠COP=∠AOE+∠DOP,
∴∠COP-∠DOP =∠AOE=80°,
∵∠COP+∠DOP=180°,
∴∠COP=130°, ∠DOP=50°,
当OP在直线CD上方时(如图),

∴∠BOP=∠BOD+ ∠DOP=80°+50°=130°;

∠BOP=∠BOD- ∠DOP=80°-50°=-30°;
综上,∠BOP的度数为130°或30°.