��Ŀ����
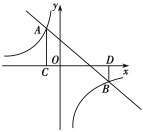
����Ŀ����ͼ��ֱ��y��![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����![]() x2+bx+c����A��B���㣬��x�������ύ�ڵ�C������BC��PΪ�߶�AC�ϵĶ��㣬P��A��C���غϣ���PQ��BC��AB�ڵ�Q��A����PQ�ĶԳƵ�ΪD������PD��QD��BD��
x2+bx+c����A��B���㣬��x�������ύ�ڵ�C������BC��PΪ�߶�AC�ϵĶ��㣬P��A��C���غϣ���PQ��BC��AB�ڵ�Q��A����PQ�ĶԳƵ�ΪD������PD��QD��BD��
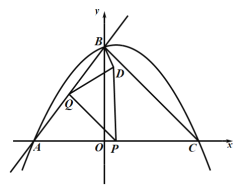
��1���������ߵĽ���ʽ��
��2������D����������ʱ�����P�����꣮
��3�����P�ĺ�����Ϊx����PDQ���ABC���ص����ֵ����ΪS
��ֱ��д��S��x�ĺ�����ϵʽ��
�ڵ���BDQΪֱ��������ʱ��ֱ��д��x��ֵ��
���𰸡���1��y����![]() x2+
x2+![]() x+4����2����P�����꣨1��0������3���ٵ�
x+4����2����P�����꣨1��0������3���ٵ�![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ���ڵ�
���ڵ�![]() Ϊֱ��������ʱ��x��ֵ��
Ϊֱ��������ʱ��x��ֵ��![]() ��
��![]() ��
��
��������
��1������һ�κ�������ʽ���A��B�������꣬Ȼ����뵽���κ�������ʽ�У��ô���ϵ������������ʽ��
��2�����P�����꣨x��0�����������߽���ʽ���C�����꣬�ɴ���á�BCO=45������ƽ���ߵĺͶԳƵ�������á�QPA=��BCO=45������APD=90�����Ӷ��õ���D�����꣨x��x+3����Ȼ����ݵ�D�����������з�����⣻
��3���ٴ���2�������һ���ǵ�D��BC����࣬��һ���ǵ�D��BC���Ҳ࣬��������������������Ĺ�ϵ����ã�
�ڷֵ���QBD=90���͡�QDB=90�������������Ϲ��ɶ�����ƽ���߷��߶γɱ����������AP�ij����Ӷ���x��ֵ��
�⣺��1����y��![]() x+4�У���x=0��y=4����y=0��x=-3
x+4����x=0��y=4����y=0��x=-3
��A��-3��0����B��0��4��
��������y����![]() x2+bx+c����A��B����
x2+bx+c����A��B����
��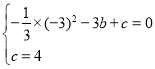
���![]()
�������ߵĽ���ʽΪy����![]() x2+
x2+![]() x+4
x+4
��2�����P�����꣨x��0��
��y����![]() x2+
x2+![]() x+4=0
x+4=0
���![]() ��
�� ![]()
����C��4��0��
��OB=OC=4
�֡� PQ��BC�ҵ�A����PQ�ĶԳƵ�ΪD��
���QPA=��DPQ=��BCO=45��
���APD=90��
�֡�A��-3��0��
���D�����꣨x��x+3��,
�������D����������
��x+3=��![]() x2+
x2+![]() x+4
x+4
���![]()
![]()
��P��A��C���غ�
���P�����꣨1��0����
�ٵ���D�պ���BC��ʱ
��B(0��4)��C(4��0)
��ֱ��BC�Ľ���ʽΪ��y=-x+4
����D�պ���BC��ʱ����D(x��-x+4)
��PD=AP
��-x+4=3+x����ã�x=![]()
���һ������D��ֱ��BC�����ʱ������![]() ʱ��ͼ�����£�
ʱ��ͼ�����£�
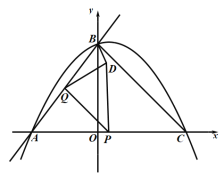
��![]()
��A(-3��0)��B(0��4)��C(4��0)
��![]()
��QP��BC
���AQP=��ABC
�ߡ�QAP=��BAC
���AQP�ס�ABC
��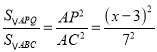
��ã�![]()
![]() ����
����![]()
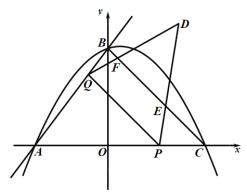
�����������D��ֱ��BC���Ҳ�ʱ������![]() ʱ��ͼ�����£�QD��BC�ڵ�F��DP��BC�ڵ�E��
ʱ��ͼ�����£�QD��BC�ڵ�F��DP��BC�ڵ�E��
��![]()
�����![]()
![]()
�ߡ�BCO=45�������QPA=��QPD=45��
���APD=90������DP��x��
���PEC�ǵ���ֱ��������
��PE=PC=4-x
��AP=x+3����PD=x+3
��ED=DP-PE=2x-1
ͬ����֪��![]() �ס�ABC
�ס�ABC
��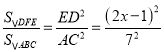
��ã�![]()
![]()
��![]()
![]() -(
-(![]() )=
)=![]()
����![]()
���ϵã���![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]()
����ͼ������AD���ɶԳ��Կ�֪AD��PQ
���D���ڹ���A��BC�Ĵ����ϣ��费��ΪE
��PQ��BC
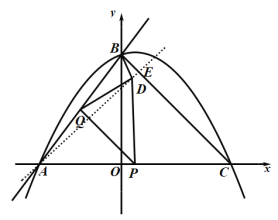
����QBD=90��ʱ��![]()
��![]()
![]() ����
����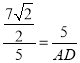
��ã�![]() ����AF=
����AF=![]()
��![]()
��![]() ����
����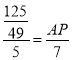
��ã�![]()
��![]()
����BDQ=90��ʱ�����Ͽ�֪��![]() ��
��![]()
����ݹ��ɶ����ɵ�![]()
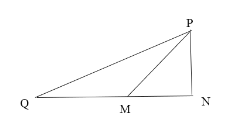
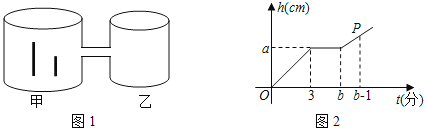
��ͼ����PQ=5��QN=![]() ��
��![]()
��QM=MP=a����![]()
���ɹ��ɶ����ɵ�![]()
��ã�![]()
��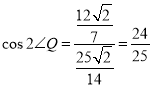
��![]()
��![]() ��
��![]() ��
��
���![]()
��![]()
����������x��ֵΪ![]() ��
��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ���ס�����У��ѡ��10��ѧ���μ�������̩����������֪ʶ������Ԥ����������ѡ�ֵijɼ����£�
����93��98��89��93�� 95��96�� 93��96��98�� 99��
����93��94��88��91��92��93��100�� 98��98��93��
ͨ���������õ����ݷ��������£�
ѧУ | ��߷� | ƽ���� | ��λ�� | ���� | ���� |
��У | 99 | a | 95.5 | 93 | 8.4 |
��У | 100 | 94 | b | 93 | c |
��1����գ�a = ��b = ��
��2���������c��ֵ������Ϊ����ѧУ�����ӳɼ��ã���д����������Ϊ�öӳɼ��õ����ɣ�