题目内容
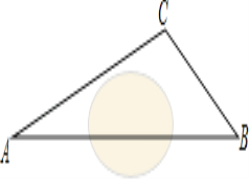
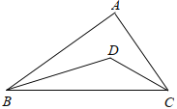
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 内,且
内,且![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作直线
作直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 与
与![]() 相似,则线段
相似,则线段![]() 的长为( )
的长为( )
A.5B.![]() C.5或
C.5或![]() D.6
D.6
【答案】B
【解析】
分△APQ∽△ABC,△APQ∽△ACB两种情况,结合相似三角形的性质和三角形内切圆求解即可.
解:若△APQ∽△ABC,
∴∠APQ=∠ABC,
∴PQ∥BC,![]() ,
,
∴∠PDB=∠DBC,
∵BD平分∠ABC,
∴∠PBD=∠CBD,
∴∠PBD =∠PDB,
∴PB=PD,同理,DQ=CQ,
∵![]() ,
,![]() ,
,![]() ,
,
∴BC=![]() ,
,
设AP=x,根据![]() 得
得![]() ,
,
∴AQ=![]() ,
,
∴PB=PD=8-x,CQ=DQ=6-![]() ,
,
∴PQ=PD+QD=![]() ,
,
∴![]() ,即
,即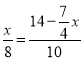 ,
,
解得:x=![]() ,
,
∴PQ=![]() ;
;
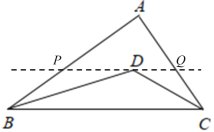
若△APQ∽△ACB,
则![]() ,
,
由题意知:D为△ABC的内心,设△ABC的内切圆交AB于M,交AC于N,
可知四边形AMDN为正方形,
∴∠A=∠AMD=∠AND=∠MDN=90°,
∴AM∥DN,AN∥DM,
∴∠MPD=∠NDQ,∠MDP=∠NQD,
∴△MPD∽△NDQ,
∴![]() ,
,
∵AB=8,AC=6,BC=10,
∴DM=DN=![]() =2,
=2,
∴AM=AN=2,
设PM=x,则![]() ,
,
∴NQ=![]() ,
,
∵![]() ,即
,即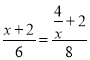 ,
,
解得:x=![]() 或-2(舍),
或-2(舍),
∴AP=![]() +2=
+2=![]() ,
,
∴PQ=AP×BC÷AC=![]() ×10÷6=
×10÷6=![]() .
.

综上:PQ的值为![]() .
.
故选B.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?