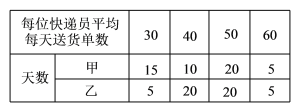题目内容
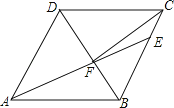
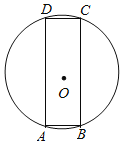
【题目】如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A′、D′,如果直线A′D′与⊙O相切,那么![]() 的值为_____.
的值为_____.
【答案】![]()
【解析】
根据题意作图,翻折找出AD=BC=A′D′,AB=CD=CD′=A′B,过O作OH⊥CD,连接OC,OG交BC于E,根据已知条件设出AB=CD=CD′=A′B=x,则OC=OG=![]() x,再由勾股定理求出CE,即可求出BC,代入求比值即可.
x,再由勾股定理求出CE,即可求出BC,代入求比值即可.
设直线A′D′与⊙O相切于G,连接OC,OG交BC于E,
∵将矩形ABCD沿着直线BC翻折,
∴AD=BC=A′D′,AB=CD=CD′=A′B,
过O作OH⊥CD,
∴CH=![]() CD,
CD,
∵直线A′D′与⊙O相切,
∴OG⊥A′D′,
∵BC∥A′D′,
∴OG⊥BC,
∴则四边形OECH是矩形,CE=BE=![]() BC,
BC,
∴CH=OE,
设AB=CD=CD′=A′B=x,
∴OE=![]() x,
x,
∴OC=OG=![]() x,
x,
∴CE=![]() =
=![]() ,
,
∴BC=2CE=![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

【题目】小明去超市采购防疫物品,超市提供下表所示![]() 、
、![]() 两种套餐,小明决定购买50份
两种套餐,小明决定购买50份![]() 套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐.超市为了促进消费,给出两种优惠方式,方式一:现金支付总额每满700元立减200元;方式二:现金支付总额每满600元送300元现金券,现金券可等同现金使用,但是使用现金券的总额不能超过应付总金额.
套餐类别 | 一次性防护口罩 | 免洗洗手液 | 套餐价格 |
| 2包 | 1瓶 | 71元 |
| 1包 | 2瓶 | 67元 |
(1)求一次性防护口罩和免洗洗手液各自的单价;
(2)小明觉得优惠方式二比方式一的优惠力度更大,他计划分两次购买,第一次付现金购买一部分![]() 套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
套餐,获得的现金券在购买剩下的部分的时候全部用掉.请你通过计算说明小明这样做能否比优惠方式一付款更省钱?
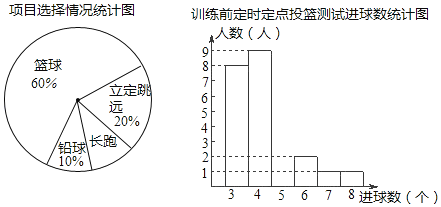
【题目】某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后郗进行了测试.现将项目选择情况及训练前后篮球定时定点投测试成绩整理作出如下统计图表.
训练后篮球定时定点投篮测试进球数统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题
(1)送择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(2)直接补全“训练前篮球定时定点投测试进球数统计图”;
(3)若全区共有该年级学生4000人,请估计参加训练后篮球定时定点投篮进球数达到6个以上(包含6个)多少人?